题目内容
设p在x轴上,它到p1(0,
,3)的距离为到点 p2(0,1,-1)的距离的两倍,点p的坐标是
| 2 |
(1,0,0),(-1,0,0)
(1,0,0),(-1,0,0)
.分析:由p在x轴上,设P(x,0,0),由P到p1(0,
,3)的距离为到点 p2(0,1,-1)的距离的两倍,知
=2
,由此能求出点p的坐标.
| 2 |
| x2+2+9 |
| x2+1+1 |
解答:解:∵p在x轴上,
∴设P(x,0,0),
∵P到p1(0,
,3)的距离为到点 p2(0,1,-1)的距离的两倍,
∴
=2
,
即x2+11=4x2+8,
∴x2=1,
∴x=±1.
∴P(1,0,0)或P(-1,0,0),
故答案为:(1,0,0),(-1,0,0).
∴设P(x,0,0),
∵P到p1(0,
| 2 |
∴
| x2+2+9 |
| x2+1+1 |
即x2+11=4x2+8,
∴x2=1,
∴x=±1.
∴P(1,0,0)或P(-1,0,0),
故答案为:(1,0,0),(-1,0,0).
点评:本题考查空间中两点间距离公式的应用,是基础题.解题时要认真审题,仔细解答.易错点是容易忽视x=-1的情况而造成丢失解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
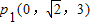 的距离为到点 p2(0,1,-1)的距离的两倍,点p的坐标是 .
的距离为到点 p2(0,1,-1)的距离的两倍,点p的坐标是 .