题目内容
设动点P(x,y)(x≥0)到定点F(| 1 |
| 2 |
| 1 |
| 2 |
(1)求点P的轨迹方程;
(2)设圆M过A(1,0),且圆心M在P的轨迹上,EF是圆M在y轴上截得的弦,当M运动时弦长|EF|是否为定值?请说明理由.
分析:(1)利用两点间的距离公式根据P到F的距离比它到y轴的距离大
,求出点P的轨迹方程即可;
(2)设圆心M(a,b),因为圆M过A(1,0),所以圆的半径为
,写出圆的方程,令x=0得到关于y的一元二次方程,利用根与系数的关系求出弦长为定值.
| 1 |
| 2 |
(2)设圆心M(a,b),因为圆M过A(1,0),所以圆的半径为
| (a-1)2+b2 |
解答:解:(1)依题意,P到F(
,0)距离比P到y轴的距离大
,即
=x+
,化简得:y2=2x,
所以曲线C是以原点为顶点,F(
,0)为焦点的抛物线P=1曲线C方程是y2=2x;
(2)设圆心M(a,b),因为圆M过A(1,0),
故设圆的方程(x-a)2+(y-b)2=(a-1)2+b2令x=0得:y2-2by+2a-1=0,
设圆与y轴的两交点为(0,y1),(0,y2),
则y1+y2=2b,y1•y2=2a-1(y1-y2)2=(y1+y2)2-4y1•y2=(2b)2-4(2a-1)=4b2-8a+4,
M(a,b)在抛物线y2=2x上,b2=2a(y1-y2)2=4|y1-y2|=2,
所以,当M运动时,弦长|EF|为定值2.
| 1 |
| 2 |
| 1 |
| 2 |
(x-
|
| 1 |
| 2 |
所以曲线C是以原点为顶点,F(
| 1 |
| 2 |
(2)设圆心M(a,b),因为圆M过A(1,0),
故设圆的方程(x-a)2+(y-b)2=(a-1)2+b2令x=0得:y2-2by+2a-1=0,
设圆与y轴的两交点为(0,y1),(0,y2),
则y1+y2=2b,y1•y2=2a-1(y1-y2)2=(y1+y2)2-4y1•y2=(2b)2-4(2a-1)=4b2-8a+4,
M(a,b)在抛物线y2=2x上,b2=2a(y1-y2)2=4|y1-y2|=2,
所以,当M运动时,弦长|EF|为定值2.
点评:考查学生会根据已知条件得到动点的轨迹方程,综合运用直线与圆的方程,以及会根据根与系数的关系解决数学问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
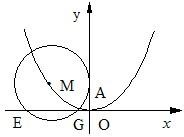 设动点P(x,y)(y≥0)到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C.
设动点P(x,y)(y≥0)到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C.