题目内容
在直角坐标系中,曲线C的参数方程为 (
( 为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点
为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点 ,直线l的极坐标方程为
,直线l的极坐标方程为 .
.
(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与曲线C的两个交点为A、B,求 的值.
的值.
(1)点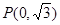 在直线
在直线 上;(2)
上;(2) .
.
解析试题分析:本题考查极坐标方程与直角坐标方程之间的转化以及直线与曲线相交问题,考查学生的转化能力和计算能力.第一问,先利用极坐标方程与直角坐标方程的互化公式将直线 的极坐标方程化为直角坐标方程,再将点
的极坐标方程化为直角坐标方程,再将点 化为直角坐标系下的点,将
化为直角坐标系下的点,将 的坐标代入直线方程中判断出点在直线上;第二问,因为直线
的坐标代入直线方程中判断出点在直线上;第二问,因为直线 与曲线
与曲线 相交,所以联立方程,消参得到关于
相交,所以联立方程,消参得到关于 的方程,再化简
的方程,再化简 代入以上得到的结论即可.
代入以上得到的结论即可.
试题解析:(1)直线 即
即
∴直线 的直角坐标方程为
的直角坐标方程为 ,点
,点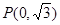 在直线
在直线 上.
上. 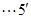
(2)直线 的参数方程为
的参数方程为 (
( 为参数),曲线C的直角坐标方程为
为参数),曲线C的直角坐标方程为
将直线 的参数方程代入曲线C的直角坐标方程,
的参数方程代入曲线C的直角坐标方程,
有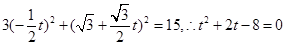 ,
,
设两根为 ,
,

考点:1.极坐标方程与直角坐标方程的互化;2.直线与曲线的相交问题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 ,直线的极坐标方程为ρcos
,直线的极坐标方程为ρcos =a,且点A在直线上.
=a,且点A在直线上. ,(α为参数),试判断直线与圆的位置关系.
,(α为参数),试判断直线与圆的位置关系. )=
)= .
. 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为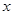 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 是参数).若直线
是参数).若直线 的值.
的值. 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆 已知曲线
是圆心在极轴上,且经过极点的圆 已知曲线 对应的参数
对应的参数 ,射线
,射线 与曲线
与曲线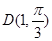
 ,
, 在曲线
在曲线 的值
的值 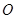 处,极轴与
处,极轴与 轴的正半轴重合,且长度单位相同.直线
轴的正半轴重合,且长度单位相同.直线 的极坐标方程为:
的极坐标方程为: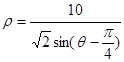 ,点
,点 ,参数
,参数 .
. 轨迹的直角坐标方程;(Ⅱ)求点
轨迹的直角坐标方程;(Ⅱ)求点 ,直线
,直线 的参数方程为
的参数方程为 ( t为参数,0≤
( t为参数,0≤ <
< ).
). 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系. 的极坐标方程是
的极坐标方程是 ,射线
,射线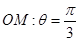 与圆
与圆 ,与直线
,与直线 ,求线段
,求线段 的长.
的长. ,点
,点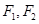 为其左,右焦点,直线
为其左,右焦点,直线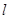 的参数方程为
的参数方程为 (
( 为参数,
为参数, ).
).