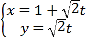题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 上的最大值为1,求实数
上的最大值为1,求实数![]() 的取值集合.
的取值集合.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)对函数![]() 求导得
求导得![]() ,对
,对![]() 分类讨论,结合导数的性质,即可得到函数
分类讨论,结合导数的性质,即可得到函数![]() 的单调性;(2)函数
的单调性;(2)函数![]() 在
在![]() 上的最大值为1等价于对任意
上的最大值为1等价于对任意![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,变形可得
恒成立,变形可得![]() ,分别对
,分别对![]() ,
,![]() 及
及![]() 讨论,即可求得实数
讨论,即可求得实数![]() 的取值集合.
的取值集合.
试题解析:(1)![]() .
.
当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() .
.
∴![]() 时,
时,![]() ,
,![]() 在
在![]() 上递减;
上递减;
![]() 时,
时,![]() ,
,![]() 在
在![]() 上递增;
上递增;
![]() 时,
时,![]() ,
,![]() 在
在![]() 上递减;
上递减;
综上,当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上递减;
上递减;
在![]() 上递增;
上递增;![]() 上递减.
上递减.
(2)∵函数![]() 在
在![]() 上的最大值为1
上的最大值为1
∴对任意![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,变形可得.
恒成立,变形可得.
当![]() 时,
时,![]() 即
即![]() ,可得
,可得![]() ;
;
当![]() 时,
时,![]() .则
.则![]()
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
因此,![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() .则
.则![]()
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,
因此,![]() ,
,
∴![]() .
.
综上,![]() .
.
∴![]() 的取值集合为
的取值集合为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
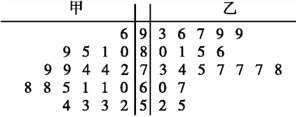
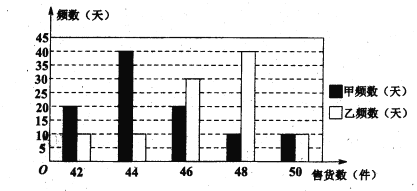
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
【答案】(I)见解析; (Ⅱ)见解析.
【解析】分析:(I)依题意可得甲公司一名推销员的工资与销售件数的关系是一次函数的关系式,而乙公司是分段函数的关系式,由此解得;(Ⅱ)分别根据条形图求得甲、乙公司一名推销员的日工资的分布列,从而可分别求得数学期望,进而可得结论.
详解:(I)由题意得,甲公司一名推销员的日工资![]() (单位:元) 与销售件数
(单位:元) 与销售件数![]() 的关系式为:
的关系式为: ![]() .
.
乙公司一名推销员的日工资![]() (单位: 元) 与销售件数
(单位: 元) 与销售件数![]() 的关系式为:
的关系式为: 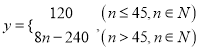
(Ⅱ)记甲公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
记乙公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴仅从日均收入的角度考虑,我会选择去乙公司.
点睛:求解离散型随机变量的数学期望的一般步骤为:
第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率;
第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值
【题型】解答题
【结束】
19
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
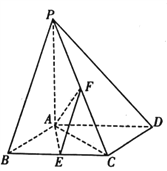
(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.