Question

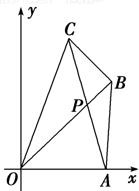如图所示，已知点A（4，0），B（4，4），C（2，6），求AC和OB的交点P的坐标．

Answer 1

分析：利用向量共线的充要条件设出

OP

，利用向量的运算法则求出

AP

，由于

AP

与

AC

共线，再利用向量共线的充要条件列出方程求出坐标

解答：解：设

OP

=t

OB

=t（4，4）=（4t，4t），
则

AP

=

OP

-

OA

=（4t，4t）-（4，0）
=（4t-4，4t），

AC

=（2，6）-（4，0）=（-2，6）．
由

AP

，

AC

共线的充要条件知（4t-4）×6-4t×（-2）=0，解得t=

3

4

．
∴

OP

=（4t，4t）=（3，3）．
∴P点坐标为（3，3）．

点评：本题考查向量的共线的充要条件、向量的坐标求法、向量的运算法则．