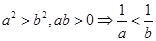题目内容
已知a,b,c∈{正实数},且a2+b2=c2,当n∈N,n>2时比较cn与an+bn的大小.
an+bn<cn.
解:∵a,b,c∈{正实数},∴an,bn,cn>0,
而 =(
=( )n+(
)n+(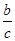 )n.
)n.
∵a2+b2=c2,则( )2+(
)2+(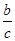 )2=1,
)2=1,
∴0< <1,0<
<1,0<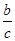 <1.
<1.
∵n∈N,n>2,
∴( )n<(
)n<( )2,(
)2,(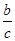 )n<(
)n<(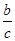 )2,
)2,
∴ =(
=( )n+(
)n+(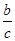 )n<
)n< =1,
=1,
∴an+bn<cn.
而
 =(
=( )n+(
)n+(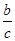 )n.
)n.∵a2+b2=c2,则(
 )2+(
)2+(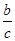 )2=1,
)2=1,∴0<
 <1,0<
<1,0<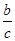 <1.
<1.∵n∈N,n>2,
∴(
 )n<(
)n<( )2,(
)2,(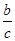 )n<(
)n<(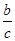 )2,
)2,∴
 =(
=( )n+(
)n+(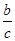 )n<
)n< =1,
=1,∴an+bn<cn.

练习册系列答案
相关题目
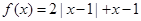 ,
,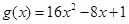 ,记
,记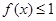 的解集为M,
的解集为M,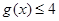 的解集为N.
的解集为N.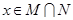 时,证明:
时,证明: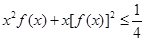 .
. 并指明等号何时成立.
并指明等号何时成立. 
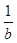 -
-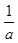 =1,则a-b<1;
=1,则a-b<1;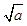 -
-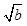 |=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.
|=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.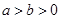 ,
,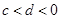 ,则一定有( )
,则一定有( )



 <α<β<
<α<β<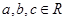 ,则下列推证中正确的是( )
,则下列推证中正确的是( )