题目内容
已知各项都为正数的等比数列{an}满足:a7=a6+2a5,若存在两项am,an,使得
=4a1,则m(1+n)的最大值等于
| am•an |
12
12
.分析:由条件求得q=2,再由
=4a1,求得m+n=6,再根据 m(1+n)=(6-n)(1+n),利用二次函数的性质可得m(1+n)的最大值.
| am•an |
解答:解:设等比数列{an}的首项为a1,公比为q,∵a7=a6+2a5,则a1•q6=a1•q5+2a1•q4,即q2-q-2=0,解得q=2或q=-1(舍去).
∵
=4a1,故有a12×2m+n-2=16 a12,则m+n=6.
则m(1+n)=(6-n)(1+n),利用二次函数的性质可得,当n=3时,m(1+n)取得最大值为12,
故答案为 12.
∵
| am•an |
则m(1+n)=(6-n)(1+n),利用二次函数的性质可得,当n=3时,m(1+n)取得最大值为12,
故答案为 12.
点评:本题考查的知识点是等比数列的性质,基本不等式,其中得到m+n=6,m(1+n)=(6-n)(1+n),是解题的关键,属于中档题.

练习册系列答案
相关题目
 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈ ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是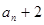 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈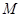 ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 是an+2 和an的等比中项.
是an+2 和an的等比中项. +
+ +…+
+…+ <1;
<1; 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个?