题目内容
若两个函数的图象只经过若干次平移后就能够重合,则称这两个函数为“同形”函数.给出下列函数:①f1(x)=sinx+cosx,②f2(x)=sinx,③f3(x)=
sinx+
,④f4(x)=
(sinx+cosx),其中“同形”函数有______.(填序号)
| 2 |
| 2 |
| 2 |
①f1(x)=sinx+cosx=
sin(x+
),④f4(x)=
(sinx+cosx)=2sin(x+
)
只有①和③中函数的解析式的振幅相同,故可排除②和④
函数f1(x)=
sin(x+
)先向右平移
个单位得f(x)=
sinx,
再向上平移
个单位得到函数f(x)=
sinx+
与③重合,
故①③为“同形”函数
故答案为:①③.
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
只有①和③中函数的解析式的振幅相同,故可排除②和④
函数f1(x)=
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
再向上平移
| 2 |
| 2 |
| 2 |
故①③为“同形”函数
故答案为:①③.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
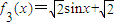 ,④
,④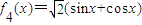 ,其中“同形”函数有 .(填序号)
,其中“同形”函数有 .(填序号) ,④
,④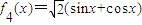 ,其中“同形”函数有 .(填序号)
,其中“同形”函数有 .(填序号)