题目内容
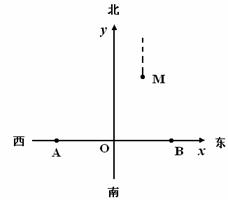
如图,相距200海里的A、B两地分别有救援A船和B船.在接到求救信息后,A船能立即出发,B船因港口原因需2小时后才能出发,两船的航速都是30海里/小时.在同时收到求救信息后,A船早于B船到达的区域称为A区,否则称为B区.若在A地北偏东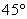 方向,距A地
方向,距A地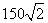 海里处的
海里处的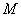 点有一艘遇险船正以10海里/小时的速度向正北方向漂移.
点有一艘遇险船正以10海里/小时的速度向正北方向漂移.
⑴求A区与B区边界线(即A、B两船能同时到达的点的轨迹)方程;
⑵问:
①应派哪艘船前往救援?
②救援船最快需多长时间才能与遇险船相遇?(精确到 小时)
小时)
解:⑴设点 为边界线上的点,由题意知
为边界线上的点,由题意知 ,即
,即 ,
,
即动点 到两定点
到两定点 、
、 的距离之差为常数,
的距离之差为常数,
∴点 的轨迹是双曲线中的一支。 由
的轨迹是双曲线中的一支。 由 得
得 ,
,
∴方程为 (
( )
)
⑵①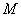 点的坐标为
点的坐标为 ,
, 点的坐标为
点的坐标为 ,
, 点的坐标为
点的坐标为 ,∴
,∴ ,
, ,
, ,∴点
,∴点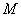 在A区,又遇险船向正北方向漂移,,即遇险船始终在A区内,∴应派A船前往救援
在A区,又遇险船向正北方向漂移,,即遇险船始终在A区内,∴应派A船前往救援
②设经 小时后,A救援船在点
小时后,A救援船在点 处与遇险船相遇。在
处与遇险船相遇。在 中,
中, ,
,
∴
整理得 ,
,
解得 或
或 (舍)
(舍)
∴A救援船需 小时后才能与遇险船相遇.
小时后才能与遇险船相遇.

练习册系列答案
相关题目

 和曲线
和曲线 恰有六个公共点,则
恰有六个公共点,则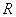 的值是 .
的值是 . ,且
,且 ,则下列不等式中,正确的是
,则下列不等式中,正确的是 B.
B. C.
C. D.
D.
 <0,那么角
<0,那么角 是( ).
是( ). ABC中,
ABC中, ,
, ,则
,则 的值等于( )
的值等于( ) 或
或 (B)
(B)  或
或
 ,若数列
,若数列 满足
满足
 ,且
,且 的取值范围是( )
的取值范围是( ) (B)
(B) (C)
(C)  (D)
(D) 
 ]上单调递增,则ω的取值范围是_________.
]上单调递增,则ω的取值范围是_________.