题目内容
已知函数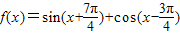
，x∈R．（1）求f（x）的最小正周期和最小值；
（2）已知
，
，
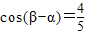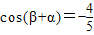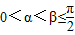，求f（β）的值．
【答案】分析：（1）由辅助角公式对已知函数化简可得，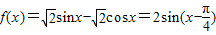
，结合正弦函数的性质可求周期、函数的最大值
（2）由已知利用和角与差角的余弦公式展开可求得cosαcosβ=0，结合已知角α，β的范围可求β，代入可求f（β）的值．
解答：解：（1）∵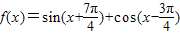
=sinxcos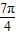
=
∴
，
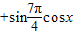
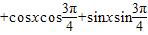
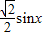
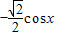
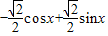
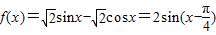∴T=2π，f（x）max=2
（2）∵
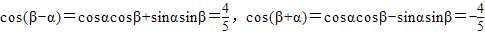
∴cosαcosβ=0
∵
，
∴
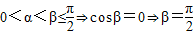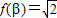
点评：本题主要考查了辅助角公式在三角函数的化简中的应用，正弦函数的性质的应用，两角和与差的余弦公式的应用．
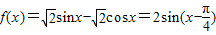，结合正弦函数的性质可求周期、函数的最大值（2）由已知利用和角与差角的余弦公式展开可求得cosαcosβ=0，结合已知角α，β的范围可求β，代入可求f（β）的值．
解答：解：（1）∵
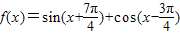
=sinxcos
=
∴
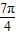
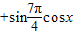
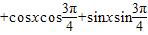
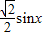
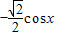
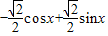
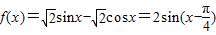，∴T=2π，f（x）max=2
（2）∵
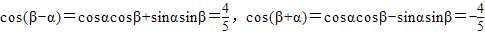
∴cosαcosβ=0
∵
，∴
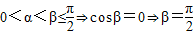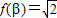
点评：本题主要考查了辅助角公式在三角函数的化简中的应用，正弦函数的性质的应用，两角和与差的余弦公式的应用．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
相关题目
（x∈R）．若
，
．求cos2x的值．
，x∈R，且
，
，
，求cos（α+β）的值．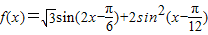
（x∈R）．
，x∈R
，x∈R，且
，
，
，求cos（α+β）的值．