题目内容
17.在△ABC中,AB=2,AC=3,$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$,则$\overrightarrow{AD}$•$\overrightarrow{BD}$=( )| A. | -$\frac{5}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{5}{4}$ | D. | $\frac{5}{4}$ |
分析 根据题意,画出图形,结合图形,用向量$\overrightarrow{AC}$、$\overrightarrow{AB}$表示出$\overrightarrow{AD}$与$\overrightarrow{BD}$,再求它们的数量积.
解答 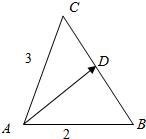 解:如图所示,△ABC中,AB=2,AC=3,
解:如图所示,△ABC中,AB=2,AC=3,
∴$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$($\overrightarrow{AC}$-$\overrightarrow{AB}$),
∴D是BC的中点,
∴$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AB}$);
∴$\overrightarrow{AD}$•$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AB}$)•$\frac{1}{2}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)
=$\frac{1}{4}$(${\overrightarrow{AC}}^{2}$-${\overrightarrow{AB}}^{2}$)
=$\frac{1}{4}$×(32-22)
=$\frac{5}{4}$.
故选:D.
点评 本题考查了平面向量的线性表示与数量积的应用问题,是基础题目.

练习册系列答案
相关题目
12.已知tanx=$\frac{1}{3}$,则sin2x=( )
| A. | $\frac{\sqrt{3}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
2.已知a=3${\;}^{\frac{1}{3}}$,b=log${\;}_{\frac{1}{2}}$3,c=log${\;}_{\frac{1}{3}}$$\frac{1}{2}$,则( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
9.已知函数f(x)=$\frac{1+lnx}{x}$在区间(a,a+$\frac{2}{3}$)(a>0)上存在极值,则实数a的取值范围是( )
| A. | (0,1) | B. | ($\frac{1}{3}$,1) | C. | ($\frac{1}{2}$,1) | D. | ($\frac{2}{3}$,1) |
6.如果实数x,y满足x2+y2=4,那么$\frac{y-2}{x+3}$的最小值是( )
| A. | -$\frac{12}{5}$ | B. | -1 | C. | -$\frac{5}{12}$ | D. | 0 |
7.已知$a={log_3}\frac{1}{2},b={2^{0.01}},c=ln\frac{1}{2}$,则a,b,c的大小关系为( )
| A. | b>a>c | B. | b>c>a | C. | a>c>b | D. | a>b>c |
 正三棱台的高为3,上、下底面边长分别为2和4,求这个棱台的侧棱长和斜高.
正三棱台的高为3,上、下底面边长分别为2和4,求这个棱台的侧棱长和斜高.