题目内容
7.已知$a={log_3}\frac{1}{2},b={2^{0.01}},c=ln\frac{1}{2}$,则a,b,c的大小关系为( )| A. | b>a>c | B. | b>c>a | C. | a>c>b | D. | a>b>c |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵b=20.01>1,0>$a=lo{g}_{3}\frac{1}{2}$=-log32>-ln2=c,
∴b>a>c.
故选:A.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.在△ABC中,AB=2,AC=3,$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$,则$\overrightarrow{AD}$•$\overrightarrow{BD}$=( )
| A. | -$\frac{5}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{5}{4}$ | D. | $\frac{5}{4}$ |
19.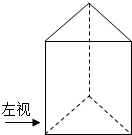 如图,侧棱长为2a的正三棱柱的左视图的面积为$\sqrt{3}$a2,则该正三棱柱的侧面积为( )
如图,侧棱长为2a的正三棱柱的左视图的面积为$\sqrt{3}$a2,则该正三棱柱的侧面积为( )
 如图,侧棱长为2a的正三棱柱的左视图的面积为$\sqrt{3}$a2,则该正三棱柱的侧面积为( )
如图,侧棱长为2a的正三棱柱的左视图的面积为$\sqrt{3}$a2,则该正三棱柱的侧面积为( )| A. | 3a2 | B. | 4a2 | C. | 6a2 | D. | 8a2 |
16.P为边长为2的正三角形内(不包括边界)一点,P到三角形三边距离分别为a、b、c,则ab+bc+ca取值范围是( )
| A. | (0,1] | B. | (0,2) | C. | $({0,2\sqrt{3}})$ | D. | (0,4) |