题目内容
10.已知弹簧拉长0.02m需要98N的力,则把弹簧拉长0.1m所做的功为( )| A. | 24.5J | B. | 23.5J | C. | 22.5J | D. | 25.0J |
分析 根据条件及胡克定律便可求出k=4900,从而便得到W=∫0.104900xdx,求该定积分即可得出把弹簧拉长0.1m所做的功.
解答 解:根据胡克定律F=kx得,$k=\frac{F}{x}=\frac{98}{0.02}=4900$;
∴把弹簧拉长0.1m所做的功为W=∫0.104900xdx=2450x2|0.10=24.5.
故选:A.
点评 考查弹簧的伸长长度和所受的拉力成正比,清楚胡克定律的内容,以及定积分求对弹簧做功的方法,会定积分的计算.

练习册系列答案
相关题目
1.已知函数g(x)的图象与函数f(x)=|ln(x+a)|-1的图象关于原点对称,且两个图象恰有三个不同的交点,则实数a的值为( )
| A. | $\frac{1}{e}$ | B. | 1 | C. | e | D. | e2 |
15.卖水果的某个体户,在不下雨的日子可赚100元,在雨天则要损失10元,该地区每年下雨的日子约有130天,则该个体户每天获利的均值是(1年按365天计算)( )
| A. | 90元 | B. | 45元 | C. | 55元 | D. | 60.82元 |
19.sin50°cos35°+sin40°sin(-35°)=( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | D. | $-\frac{\sqrt{6}+\sqrt{2}}{4}$ |
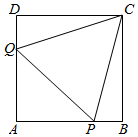 某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.
某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.