题目内容
【题目】已知函数![]() ,若点
,若点![]() 在
在![]() 的图像上运动,则点
的图像上运动,则点![]() 在
在![]() 的图象上运动
的图象上运动
(1)求![]() 的最小值,及相应的
的最小值,及相应的![]() 值
值
(2)求函数![]() 的解析式,指出其定义域
的解析式,指出其定义域![]() ,判断并证明
,判断并证明![]() 在
在![]() 上的单调性
上的单调性
(3)在函数![]() 和
和![]() 的图象上是否分别存在点
的图象上是否分别存在点![]() 关于直线
关于直线![]() 对称,若存在,求出点
对称,若存在,求出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
【答案】(1)![]() 的最小值为2,对应的
的最小值为2,对应的![]() 为0;(2)
为0;(2)![]() ,定义域为
,定义域为![]() ,
,![]() ,单调递增,证明见解析;(3)存在
,单调递增,证明见解析;(3)存在![]()
【解析】
(1)写出![]() 的解析式,依据基本不等式性质即可求解;
的解析式,依据基本不等式性质即可求解;
(2)根据点的关系求出![]() 解析式,写出
解析式,写出![]() 的解析式即可判断单调性;
的解析式即可判断单调性;
(3)设![]() 两点的坐标根据位置和对称关系列方程组求解.
两点的坐标根据位置和对称关系列方程组求解.
(1)![]() ,当且仅当
,当且仅当![]() 即
即![]() 时,等号成立,即
时,等号成立,即![]() 的最小值为2,对应的
的最小值为2,对应的![]() 为0.
为0.
(2)设![]() 图象上点
图象上点![]() ,由题:
,由题: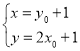 ,所以
,所以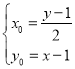
点![]() 在
在![]() 的图像上运动,则
的图像上运动,则![]() ,
,
所以![]() ,
,![]() ,由
,由![]() 得其定义域为
得其定义域为![]()
所以![]() ,定义域为
,定义域为![]()
![]() 在定义域内为增函数,证明如下:
在定义域内为增函数,证明如下:
任取![]() ,根据指数函数和对数函数单调性有:
,根据指数函数和对数函数单调性有:
![]() ,
,![]() ,
,
![]()
![]() ,
,
即![]()
所以![]() 在定义域内是增函数.
在定义域内是增函数.
(3)假设函数![]() 和
和![]() 的图象上分别存在点
的图象上分别存在点![]() 关于直线
关于直线![]() 对称,
对称,
设其坐标![]() ,则有:
,则有:
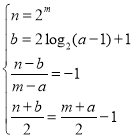 解得:
解得: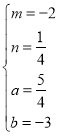
故在函数![]() 和
和![]() 的图象上分别存在点
的图象上分别存在点![]() 关于直线
关于直线![]() 对称.
对称.

练习册系列答案
相关题目