题目内容
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 且与
且与![]() 轴不重合的直线交椭圆
轴不重合的直线交椭圆![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() ,.求证:以
,.求证:以![]() 为直径的圆恒过交点
为直径的圆恒过交点![]() ,
,![]() ,并求出
,并求出![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)根据点![]() 在椭圆
在椭圆![]() 上,且△
上,且△![]() 的面积为
的面积为![]() ,结合性质
,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的方程;(Ⅱ)直线
的方程;(Ⅱ)直线![]() 的方程为
的方程为![]() ,设点
,设点![]() (不妨设
(不妨设![]() ),则点
),则点![]() ,由
,由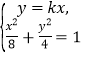 ,消去
,消去![]() 得
得![]() ,所以
,所以![]() ,
,![]() ,可证明
,可证明![]() ,
,![]() ,同理
,同理![]() ,则以
,则以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,
,![]() ,可得
,可得![]() ,进而可得结果.
,进而可得结果.
试题解析:(Ⅰ)![]() ,
,![]() ,
,
又点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,
,![]() ,
,
解得![]() ,或
,或![]() (舍去),又
(舍去),又![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)![]() ,
,![]() ,
,![]() ,
,
方法一:当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,
,![]() 为短轴的两个端点,则
为短轴的两个端点,则![]() ,
,![]() ,
, ![]() ,
,![]() ,则以
,则以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,
,![]() ,
,
当![]() 的斜率存在且不为零,设直线
的斜率存在且不为零,设直线![]() 的方程为
的方程为![]() ,
,
设点![]() (不妨设
(不妨设![]() ),则点
),则点![]() ,
,
由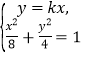 ,消去
,消去![]() 得
得![]() ,所以
,所以![]() ,
,![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
因为直线![]() 与
与![]() 轴交于点
轴交于点![]() ,令
,令![]() 得
得![]() ,
,
即点![]() ,同理可得点
,同理可得点![]() ,
,
![]() ,
,![]() ,
,
![]() ,同理
,同理![]() ,
,
则以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,
,![]() ,
,
当![]() 的斜率存在且不为零时,
的斜率存在且不为零时,
![]() ,
,
![]() △
△![]() 面积为
面积为![]() ,
,
又当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,△
,△![]() 面积为
面积为![]() ,
,
![]() △
△![]() 面积的取值范围是
面积的取值范围是![]() .
.
方法二:当![]() ,
,![]() 不为短轴的两个端点时,设
不为短轴的两个端点时,设![]() ,
,
则![]() ,由点
,由点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,令
,令![]() 得
得![]() ,
,
即点![]() ,同理可得点
,同理可得点![]() ,
,
以![]() 为直径的圆可化为
为直径的圆可化为![]() ,
,
代入![]() ,化简得
,化简得![]() ,
,
令![]() 解得
解得![]()
![]() 以
以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() △
△![]() 面积为
面积为![]() ,
,
当![]() ,
,![]() 为短轴的两个端点时,
为短轴的两个端点时,![]() ,△
,△![]() 面积为
面积为![]() ,
,
![]() △
△![]() 面积的取值范围是
面积的取值范围是![]() .
.

练习册系列答案
相关题目