题目内容
已知 为抛物线
为抛物线 的焦点,点
的焦点,点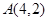 为抛物线内一定点,点
为抛物线内一定点,点 为抛物线上一动点,
为抛物线上一动点, 最小值为8.
最小值为8.
(1)求该抛物线的方程;
(2)若直线 与抛物线交于
与抛物线交于 、
、 两点,求
两点,求 的面积.
的面积.
【答案】
(1) .(2)
.(2)
【解析】
试题分析:(1)设 为点
为点 到
到 的距离,则由抛物线定义,
的距离,则由抛物线定义, ,
,
所以当点 为过点
为过点 且垂直于准线的直线与抛物线的交点时,
且垂直于准线的直线与抛物线的交点时,
 取得最小值,即
取得最小值,即 ,解得
,解得
∴抛物线的方程为 .
.
(2)设 ,联立
,联立 得
得 ,
,
显然 ,
,
 ,
,

 .
.
又
 到直线
到直线 的距离为
的距离为 ,
,

考点:本题主要考查抛物线的定义,直线与抛物线的位置关系,点到直线的距离公式,三角形面积公式。
点评:中档题,涉及“抛物线内一定点,点 为抛物线上一动点,求
为抛物线上一动点,求 最小值”问题,往往利用抛物线定义,“化折为直”。涉及抛物线与直线位置关系问题,往往利用韦达定理。
最小值”问题,往往利用抛物线定义,“化折为直”。涉及抛物线与直线位置关系问题,往往利用韦达定理。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 为抛物线
为抛物线 的焦点,抛物线上点
的焦点,抛物线上点 满足
满足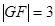
 的方程;
的方程; 点的坐标为(
点的坐标为( ,
, ),过点F作斜率为
),过点F作斜率为 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, ,连结
,连结 、
、 并延长交抛物线于
并延长交抛物线于 、
、 两点,设直线
两点,设直线 的斜率为
的斜率为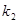 ,问
,问 是否为定值,若是求出该定值,若不是说明理由.
是否为定值,若是求出该定值,若不是说明理由. 为抛物线
为抛物线 的焦点,点
的焦点,点 为其上一点,点M与点N关于x轴对称,直线
为其上一点,点M与点N关于x轴对称,直线 与抛物线交于异于M,N的A,B两点,且
与抛物线交于异于M,N的A,B两点,且
 面积最小的直线
面积最小的直线 ,若存在,求出直线
,若存在,求出直线