题目内容
函数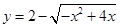 的值域是( )
的值域是( )
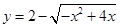 的值域是( )
的值域是( )A. | B. | C. | D. |
B
本题考查函数的三要素及函数的单调性.
由 得:
得: 所以函数的定义域为
所以函数的定义域为 设
设 ,在
,在 上是增函数,在
上是增函数,在 上是减函数;
上是减函数; 时,
时, 取最大值4;
取最大值4; 时,
时, 取最小值0;所以
取最小值0;所以 则
则 则
则 即函数的值域为
即函数的值域为 故选B
故选B
点评:与函数有关的问题,要注意定义域优先的原则.
由
 得:
得: 所以函数的定义域为
所以函数的定义域为 设
设 ,在
,在 上是增函数,在
上是增函数,在 上是减函数;
上是减函数; 时,
时, 取最大值4;
取最大值4; 时,
时, 取最小值0;所以
取最小值0;所以 则
则 则
则 即函数的值域为
即函数的值域为 故选B
故选B点评:与函数有关的问题,要注意定义域优先的原则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和函数
和函数 ,
, ,无论b取何值,函数
,无论b取何值,函数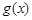 在定义域内不可能总为增函数;
在定义域内不可能总为增函数; ,线段AB的中点为
,线段AB的中点为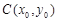 ,记直线AB的斜率为
,记直线AB的斜率为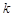 ,①对于函数
,①对于函数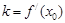 ;②对于函数
;②对于函数 ,是否具有与①同样的性质?证明你的结论.
,是否具有与①同样的性质?证明你的结论.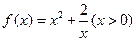 的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.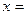 时,
时, ;
;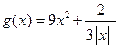 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明) 且存在
且存在 使
使
 是R上的单调增函数;
是R上的单调增函数; 其中
其中 


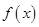 是定义在
是定义在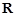 上的奇函数,且当
上的奇函数,且当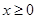 时,
时,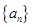 是等差数列,且
是等差数列,且 ,则
,则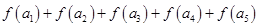 的值( )
的值( ) =
= 在区间
在区间 上是减函数. (14分)
上是减函数. (14分) 的单调递增区间为
的单调递增区间为 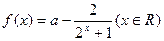
 ,求实数
,求实数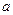 的值;
的值;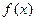 的值域
的值域 上定义在R上的奇函数,且当
上定义在R上的奇函数,且当 时,
时, ,若
,若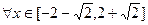 ,不等式
,不等式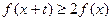 恒成立,则实数
恒成立,则实数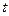 的取值范围是
的取值范围是