题目内容
4.已知函数f(x)=aln(x+1)+$\frac{1}{x+1}$+2x-1.(1)当a=2时,求函数y=f(x)的图象在x=0处的切线方程;
(2)当x≥0时,f(x)≥0恒成立,求实数a的取值范围.
分析 (1)先求函数的定义域,把a=2代入函数解析式,求导,得单调区间;
(2)令t=x+1,若x≥0时,则t≥1函数f(x)=aln(x+1)+$\frac{1}{x+1}$+2x-1=alnt+$\frac{1}{t}$+2t-3.x≥0时,f(x)≥0恒成立,等价于t≥1时,alnt+$\frac{1}{t}$+2t-3≥0.令g(t)=alnt+$\frac{1}{t}$+2t-3.对函数g(t)求导,研究g(t)即可.
解答 解:(1)函数的定义域为(-1,+∞)
当a=2时,f(x)=2ln(x+1)+$\frac{1}{x+1}$+2x-1,
f′(x)=$\frac{2}{x+1}$-$\frac{1}{{(x+1)}^{2}}$+2,
f′(0)=2-1+2=3,f(0)=0,
∴过(0,0)斜率是3的直线方程是:y=3x;
(2)令t=x+1,若x≥0时,则t≥1,
函数f(x)=aln(x+1)+$\frac{1}{x+1}$+2x-1=alnt+$\frac{1}{t}$+2t-3.
x≥0时,f(x)≥0恒成立,等价于t≥1时,alnt+$\frac{1}{t}$+2t-3≥0.
令g(t)=alnt+$\frac{1}{t}$+2t-3.
g(1)=0+1+2-3=0
g′(t)=$\frac{a}{t}$-$\frac{1}{{t}^{2}}$+2=$\frac{{2t}^{2}+at-1}{{t}^{2}}$,
设h(t)=2t2+at-1
则h(t)恒过(0,-1)
①当h(1)≥0,画函数y=h(t)的图象如图: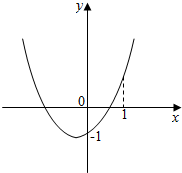
故当h(1)≥0,即2+a-1≥0,也即a≥-1时,h(t)≥0在t≥1恒成立,
∴g′(t)≥0在t≥1恒成立,
∴g(t)在t≥1时递增,∴g(t)≥g(1)=0恒成立,
②当h(1)<0时,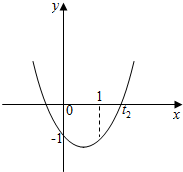
即当h(1)<0,即2+a-1<0,也即a<-1时,h(t)<0在t∈(1,t2)恒成立,
∴g′(t)<0在t∈(1,t2)恒成立,
∴g(t)在t∈(1,t2)时递减,∴g(t)<g(1)=0恒成立,不满足g(t)>0恒成立,
综上a≥-1.
点评 本题主要研究函数与导数的关系,情况复杂时,可以进行分类讨论,同时结合图象解题也是常用方法.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | (1,5) | B. | (l,-5) | C. | (-1,5) | D. | (-1,-5) |
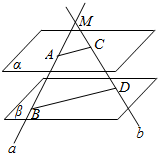 如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.
如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.