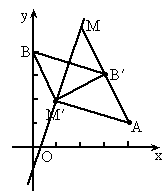题目内容
在直线
l:3x-y-1=0上求一点P,使得:(1)P
到A(4,1)和B(0,4)的距离之差最大;(2)P
到A(4,1)和C(3,4)的距离之和最小.
答案:略
解析:
提示:
解析:
|
解: (1)如图所示,设点B关于l的对称点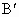 的坐标为(a,b), 的坐标为(a,b),
则 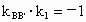 ,即 ,即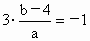 , ,
∴a +3b-12=0. ①又由于 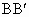 的中点坐标为M 的中点坐标为M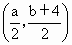 ,且在直线l上,∴ ,且在直线l上,∴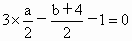 ,即3a-b-6=0. ② ,即3a-b-6=0. ②
解 ①②得a=3,b=3,∴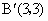 . .
于是  : :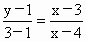 ,即2x+y-9=0. ,即2x+y-9=0.
解由 l与 的方程组得x=2,y=5,即l与 的方程组得x=2,y=5,即l与 的交点是(2,5),所以P(2,5). 的交点是(2,5),所以P(2,5).
(2) 如图所示,设C关于l的对称点为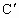 ,求出 ,求出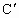 的坐标为 的坐标为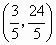 . .
所以 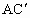 所在直线的方程为19x+17y-93=0, 所在直线的方程为19x+17y-93=0,
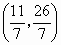 . .
故 Q点坐标为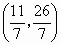 . .
|
提示:
|
设 B关于l的对称点
对于(2),若
|

练习册系列答案
相关题目


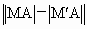 最大,求M的坐标及最大值
最大,求M的坐标及最大值