Question

如图所示，已知平面上两点A(4，1)，B(0，4)，在直线l：3x－y－1＝0上找一点M，使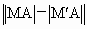最大，求M的坐标及最大值

Answer 1

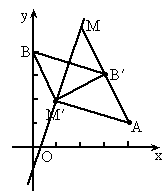
答案：略
解析：

思维分析：要求两线段之差的最大值，应借助于数形结合，利用三点共线来解决． 解：设B(0，4)关于直线l的对称点为， 则 解得 ∴．设为l上任一点，则在，中，有≤(当且仅当，，A三点共线时，等号成立，此时取最大值)． ∴过点A(4，1)，(3，3)的直线为 即2x＋y－9=0． ∴直线与直线l的交点M的坐标为方程组 的解 ∴M点的坐标为(2，5)时，取最大值，为． 点拨：利用三角形中，两边之和大于第三边这个条件得出不等式．