题目内容
（2009•济宁一模）已知双曲线
-
=1的左、右焦点分别为F1、F2，P是双曲线上的一点，若|
+
|=10，则
•
=
| x2 |
| 9 |
| y2 |
| 16 |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
0
0
．分析：根据△PF1F2中PO是中线，得到向量
等于向量
、
和的一半，结合已知条件|
+
|=10可得向量
的长度等于5，然后根据双曲线方程计算出双曲线的焦距等于10，从而得到△PF1F2是以P为直角顶点的直角三角形，得到向量
、
互相垂直，结合数量积的公式可得
•
=0．
| PO |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
| PO |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
解答：解：∵F1、F2分别是双曲线的左、右焦点
∴△PF1F2中，PO是中线
∴向量
=
（
+
）
∵|
+
|=10
∴|
|=
×10=5
∵双曲线
-
=1中，a2=9，b2=16
∴c=
=5⇒F1F2=10
∴△PF1F2中，中线PO等于F1F2的一半
∴△PF1F2是以P为直角三角形，且∠F1PF2=90°
∴
•
=
•
cos∠F1PF2=0
故答案为：0
∴△PF1F2中，PO是中线
∴向量
| PO |
| 1 |
| 2 |
| PF1 |
| PF2 |
∵|
| PF1 |
| PF2 |
∴|
| PO |
| 1 |
| 2 |
∵双曲线
| x2 |
| 9 |
| y2 |
| 16 |
∴c=
| a2+b2 |
∴△PF1F2中，中线PO等于F1F2的一半
∴△PF1F2是以P为直角三角形，且∠F1PF2=90°
∴
| PF1 |
| PF2 |
| |PF1| |
| |PF2| |
故答案为：0
点评：本题以双曲线中的向量问题为载体，着重考查了双曲线的基本概念、向量的数量积和直角三角形的判定等知识点，属于中档题．
练习册系列答案
相关题目
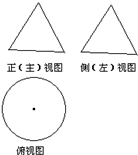（2009•济宁一模）一个几何体的三视图如图所示，其中正视图与侧视图都是边长为2的正三角形，则这个几何体的侧面积为（ ）
（2009•济宁一模）如图，在三棱柱ABC-A1B1C1中，所有的棱长都为2，∠A1AC=60°