题目内容
函数 在(0,1)上为减函数,则实数a的取值范围( )
在(0,1)上为减函数,则实数a的取值范围( )A.

B.(1,2)
C.(1,2]
D.

【答案】分析:由对数函数的性质可得,a>0,令g(x)=2-ax2,g(x)为减函数,由复合函数的性质可知a>1,又2-a≥0,从而可得答案.
解答:解:由题意得:a>0,令g(x)=2-ax2,则g(x)为减函数,
又f(x)= 在(0,1)上为减函数,
在(0,1)上为减函数,
∴a>1.①
又当x∈(0,1)时,g(x)=2-ax2>0,
∴当x=1时,g(1)=2-a≥0,
∴a≤2②
由①②得:1<a≤2.
故选C.
点评:本题考查复合函数的性质与应用,由题意得到a>1,2-a≥0是关键,也是难点,考查综合分析与理解应用的能力,属于难题.
解答:解:由题意得:a>0,令g(x)=2-ax2,则g(x)为减函数,
又f(x)=
 在(0,1)上为减函数,
在(0,1)上为减函数,∴a>1.①
又当x∈(0,1)时,g(x)=2-ax2>0,
∴当x=1时,g(1)=2-a≥0,
∴a≤2②
由①②得:1<a≤2.
故选C.
点评:本题考查复合函数的性质与应用,由题意得到a>1,2-a≥0是关键,也是难点,考查综合分析与理解应用的能力,属于难题.

练习册系列答案
相关题目
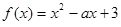 在(0,1)上为减函数,函数
在(0,1)上为减函数,函数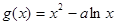 的(1,2)上为增函数,则a的值等于
的(1,2)上为增函数,则a的值等于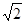 D.0
D.0 在(0,1)上为减函数,则实数a的取值范围( )
在(0,1)上为减函数,则实数a的取值范围( )

 在(0,1)上为减函数,则实数a的取值范围( )
在(0,1)上为减函数,则实数a的取值范围( )
