题目内容
(本小题满分14分)已知函数 (
( ).
).

(1)若 为函数
为函数 的极值点,求
的极值点,求 的值;
的值;
(2)若 ,
,
 已知
已知
 ,
,
 ,若直线
,若直线 、
、 及直线
及直线 与函数
与函数 的图象所围成的封闭图形如阴影部分所示,求阴影面积
的图象所围成的封闭图形如阴影部分所示,求阴影面积 关于
关于 的函数
的函数 的最小值
的最小值 ;
;
 证明不等式:
证明不等式: .
.
(1) ,(2)(ⅰ)
,(2)(ⅰ) ,(ⅱ)证明见解析,
,(ⅱ)证明见解析,
【解析】
试题分析:首先利用 为极值点,则
为极值点,则 ,求出
,求出 ;由于
;由于 与
与 的交点为
的交点为 ,所以封闭图形的面积可用两个积分的和求出,设面积为
,所以封闭图形的面积可用两个积分的和求出,设面积为 对
对 求导研究函数的单调性求出最小值;最后把求出的面积最小值
求导研究函数的单调性求出最小值;最后把求出的面积最小值 代入所证不等式整理分析,把
代入所证不等式整理分析,把 看成未知数
看成未知数 构造函数
构造函数 ,对
,对 求导,研究函数的单调性,就可以证明出本题结论;
求导,研究函数的单调性,就可以证明出本题结论;
试题解析:(1) ,
,


 ,又
,又 为极值点,
为极值点, ,经检验
,经检验 符合题意,所以
符合题意,所以 ;
;
(2)(ⅰ)


 ,设
,设


 所以
所以 ,又
,又 ,所以当
,所以当 时,
时,
 单调递减;当
单调递减;当 时,
时,
 单调递增;当
单调递增;当 时,
时,


 ,
,
(ⅱ)要证明 ,
,
令 ,
,

 ,
, 则
则 在
在 递减,又
递减,又
 ,
, ;
;
考点:导数的应用

练习册系列答案
相关题目
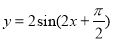 是( )
是( ) 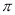 的奇函数 B.周期为
的奇函数 B.周期为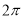 的奇函数 D.周期为
的奇函数 D.周期为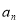 },
},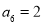 ,则此数列的前11项的和
,则此数列的前11项的和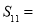
 中,若
中,若 ,则
,则 .
. ,
, ,
, ,若
,若 为实数,
为实数, ,则
,则
 B.
B. C.1 D.2
C.1 D.2 (
( ,
, ),若数列
),若数列 是等差数列,记集合
是等差数列,记集合 的元素个数为
的元素个数为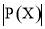 ,则
,则 关于
关于 的表达式为 .
的表达式为 . ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( ) ,
, ,
, ,则
,则
 ,
, ,且
,且 ,则
,则
 ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则
 所表示的区域内的概率为 .
所表示的区域内的概率为 . 一种各面上分别标有
一种各面上分别标有 个点的正方体玩具
个点的正方体玩具 ,观察向上的点数,则两个点数之积不小于
,观察向上的点数,则两个点数之积不小于 的概率为 .
的概率为 .