题目内容
(本题满分13分)
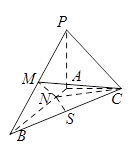
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD= .
.
(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小
(3)求点C到平面PBD的距离.
⑴见解析;(2)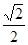 ;(3)
;(3)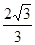 。
。
解析试题分析:方法一:⑴证:在Rt△BAD中,AD=2,BD= , ∴AB=2,ABCD为正方形,因此BD⊥AC.
, ∴AB=2,ABCD为正方形,因此BD⊥AC.
∵PA⊥平面ABCD,BDÌ平面ABCD,∴BD⊥PA .又∵PA∩AC=A ∴BD⊥平面PAC.
解:(2)由PA⊥面ABCD,知AD为PD在平面ABCD的射影,又CD⊥AD, ∴CD⊥PD,
知∠PDA为二面角P—CD—B的平面角. 又∵PA=AD,∴∠PDA=450 . 二面角P—CD—B余弦值为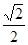 。
。
(3)∵PA=AB=AD=2,∴PB=PD=BD= ,设C到面PBD的距离为d,
,设C到面PBD的距离为d,
由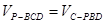 ,有
,有 ,即
,即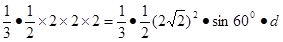 ,得
,得
方法二:证:(1)建立如图所示的直角坐标系,
则A(0,0,0)、D(0,2,0)、P(0,0,2).………………2分
在Rt△BAD中,AD=2,BD= ,
,
∴AB=2.∴B(2,0,0)、C(2,2,0),
∴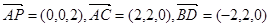
∵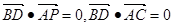 ,即BD⊥AP,BD⊥AC,又AP∩AC=A,∴BD⊥平面PAC. …………4分
,即BD⊥AP,BD⊥AC,又AP∩AC=A,∴BD⊥平面PAC. …………4分
解:(2)由(1)得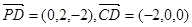 .
.
设平面PCD的法向量为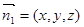 ,则
,则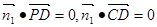 ,
,
即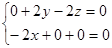 ,∴
,∴ 故平面PCD的法向量可取为
故平面PCD的法向量可取为
∵PA⊥平面ABCD,∴ 为平面ABCD的法向量. ……………………………7分
为平面ABCD的法向量. ……………………………7分
设二面角P—CD—B的大小为q,依题意可得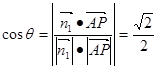 . ……………………………9分
. ……………………………9分
(3)由(Ⅰ)得 ,设平面PBD的法向量为
,设平面PBD的法向量为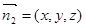 ,
,
则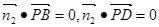 ,即
,即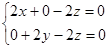 ,∴x=y=z,故可取为
,∴x=y=z,故可取为 . ………11分
. ………11分
∵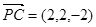 ,∴C到面PBD的距离为
,∴C到面PBD的距离为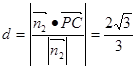 …………………13分
…………………13分
考点:本题考查直线与平面垂直的判定定理;线面垂直的性质定理;向量法求空间角; 点、线、面间的距离计算。
点评:综合法求二面角,往往需要作出平面角,这是几何中一大难点,而用向量法求解二面角无需作出二面角的平面角,只需求出平面的法向量,经过简单运算即可,从而体现了空间向量的巨大作用.二面角的向量求法: ①若AB、CD分别是二面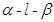 的两个半平面内与棱
的两个半平面内与棱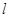 垂直的异面直线,则二面角的大小就是向量
垂直的异面直线,则二面角的大小就是向量 与
与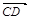 的夹角; ②设
的夹角; ②设 分别是二面角
分别是二面角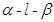 的两个面α,β的法向量,则向量
的两个面α,β的法向量,则向量 的夹角(或其补角)的大小就是二面角的平面角的大小。
的夹角(或其补角)的大小就是二面角的平面角的大小。

 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
 的长; (2)求cos<
的长; (2)求cos< >的值; (3)求证:A1B⊥C1M.
>的值; (3)求证:A1B⊥C1M.  ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
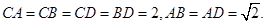

 平面BCD;
平面BCD;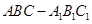 中,
中, ,
,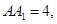 点
点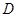 是
是 的中点。
的中点。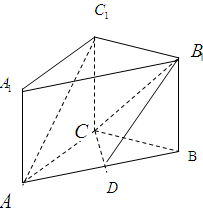

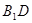 与平面
与平面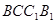 所成的角的正切值
所成的角的正切值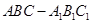 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中,  ,
, 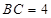 ,
, 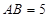 ,
,  ,点
,点 是
是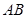 的中点.
的中点. 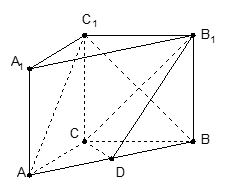
 ∥平面
∥平面 ;
;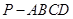 中,
中, 底面
底面 ,四边形
,四边形 ,
, ,
,  ,
, ,E为
,E为 中点.
中点.
 AB,
AB, 是⊙
是⊙ 的直径,
的直径, 垂直于⊙
垂直于⊙ 是圆周上不同于
是圆周上不同于 的任意一点,
的任意一点, .
.