题目内容
6.已知定义在R上的函数y=f(x)的导函数为f′(x),满足f′(x)<f(x),且f(0)=1,则不等式f(x)<ex的解集为( )| A. | (-∞,e4) | B. | (e4,+∞) | C. | (-∞,0) | D. | (0,+∞) |
分析 构造函数g(x)=$\frac{f(x)}{{e}^{x}}$(x∈R),研究g(x)的单调性,结合原函数的性质和函数值,即可求解.
解答 解:设g(x)=$\frac{f(x)}{{e}^{x}}$(x∈R),
则g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$,
∵f′(x)<f(x),
∴f′(x)-f(x)<0
∴g′(x)<0,
∴y=g(x)在定义域上单调递减
∵f(x)<ex
∴g(x)<1
又∵g(0)=$\frac{f(0)}{{e}^{0}}$=1
∴g(x)<g(0)
∴x>0
故选:D.
点评 本题考查函数单调性与奇偶性的结合,结合已知条件构造函数,然后用导数判断函数的单调性是解题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
16.某几何体的正视图,侧视图及俯视图均如图所示,则该几何体的体积为( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
14.函数y=$\frac{x}{x+1}$的图象是( )
| A. |  | B. |  | C. |  | D. | 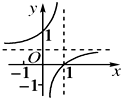 |
15.在△ABC中,∠B为钝角,则有( )
| A. | sinA>cosB | B. | sinA<cosB | ||
| C. | sinA=cosB | D. | sinA,cosB大小不确定 |
16.方程cosx=lgx的实根的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 无数 |