题目内容
求函数y=
思路分析:利用导数求切线方程的步骤:
①先求出函数y=f(x)在点x0处的导数f′(x0);
②根据直线方程的点斜式,得切线方程为y-y0=f′(x0)(x-x0).
解:欲求切线方程需先求过点P的切线的斜率K=![]() 而Δy=
而Δy=![]() (2+Δx)2-
(2+Δx)2-![]() ×22=
×22=![]() ×2Δx+
×2Δx+![]() (Δx)2,
(Δx)2,
∴![]()
∴过点p的切线方程为y-1=x-2.
即x-y-1=0.
温馨提示
f(x)在x0处的导数f′(x0),即为在该点处的切线的斜率,这是导数的几何意义.

练习册系列答案
相关题目
 ;
; ,求实数a的值;
,求实数a的值; 的旋转变换,对应的变换矩阵是M1;变换T2对应用的变换矩阵是
的旋转变换,对应的变换矩阵是M1;变换T2对应用的变换矩阵是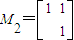 .
.