题目内容
变换T1是逆时针旋转 的旋转变换,对应的变换矩阵是M1;变换T2对应用的变换矩阵是
的旋转变换,对应的变换矩阵是M1;变换T2对应用的变换矩阵是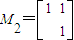 .
.(Ⅰ)求点P(2,1)在T1作用下的点P'的坐标;
(Ⅱ)求函数y=x2的图象依次在T1,T2变换的作用下所得曲线的方程.
【答案】分析:(Ⅰ)先写出时针旋转 的旋转变换矩阵M1,再利用矩阵的乘法,求出点P'的坐标;
的旋转变换矩阵M1,再利用矩阵的乘法,求出点P'的坐标;
(Ⅱ) 先求M=M2M1,再求点的变换,从而利用函数y=x2求出变换的作用下所得曲线的方程
解答:解:(Ⅰ) ,
,
所以点P(2,1)在T1作用下的点P'的坐标是P'(-1,2).…(5分)
(Ⅱ) ,
,
设 是变换后图象上任一点,与之对应的变换前的点是
是变换后图象上任一点,与之对应的变换前的点是 ,
,
则 ,
,
也就是{, ,即
,即 ,
,
所以,所求曲线的方程是y-x=y2
点评:本题以变换为载体,考查矩阵的乘法,考查点在变换下点的坐标的求法,属于中档题
 的旋转变换矩阵M1,再利用矩阵的乘法,求出点P'的坐标;
的旋转变换矩阵M1,再利用矩阵的乘法,求出点P'的坐标;(Ⅱ) 先求M=M2M1,再求点的变换,从而利用函数y=x2求出变换的作用下所得曲线的方程
解答:解:(Ⅰ)
 ,
,
所以点P(2,1)在T1作用下的点P'的坐标是P'(-1,2).…(5分)
(Ⅱ)
 ,
,设
 是变换后图象上任一点,与之对应的变换前的点是
是变换后图象上任一点,与之对应的变换前的点是 ,
,则
 ,
,也就是{,
 ,即
,即 ,
,所以,所求曲线的方程是y-x=y2
点评:本题以变换为载体,考查矩阵的乘法,考查点在变换下点的坐标的求法,属于中档题

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 ;
; ,求实数a的值;
,求实数a的值; 的旋转变换,对应的变换矩阵是M1;变换T2对应用的变换矩阵是
的旋转变换,对应的变换矩阵是M1;变换T2对应用的变换矩阵是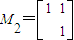 .
.