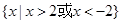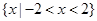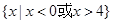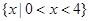题目内容
已知函数 ,曲线
,曲线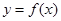 在点
在点 处切线方程为
处切线方程为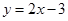 .
.
(1)求 的值;
的值;
(2)讨论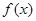 的单调性,并求
的单调性,并求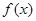 的极小值。
的极小值。
 ,曲线
,曲线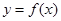 在点
在点 处切线方程为
处切线方程为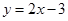 .
.(1)求
 的值;
的值;(2)讨论
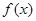 的单调性,并求
的单调性,并求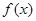 的极小值。
的极小值。(1)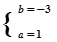 ;(2)
;(2)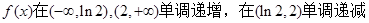 .
.
当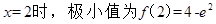 .
.
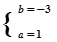 ;(2)
;(2)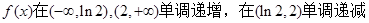 .
.当
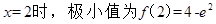 .
.试题分析:(1)对函数数求导,利用切线的斜率为2,切点为曲线与切线的交点,可得
 的值.(2)利用导函数的,构建不等式讨论
的值.(2)利用导函数的,构建不等式讨论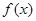 的单调性,并利用单调区间判断极值.
的单调性,并利用单调区间判断极值.试题解析:
解:
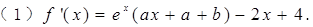 2分
2分因为在点
 处切线方程为
处切线方程为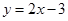 .
.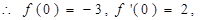
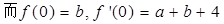
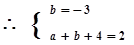 4分解得:
4分解得: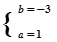 5分
5分(2)由(I)知,
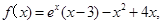
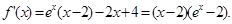 7分
7分令
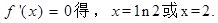 9分
9分从而当
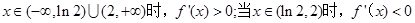 。 11分
。 11分故
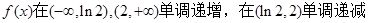 . 12分
. 12分当
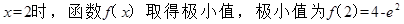 14分
14分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
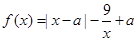 ,
,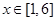 ,
,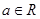 .
.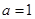 ,试判断并用定义证明函数
,试判断并用定义证明函数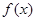 的单调性;
的单调性;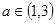 时,求证函数
时,求证函数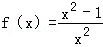 的定义域为E,值域为F.
的定义域为E,值域为F.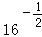 与集合F的关系;
与集合F的关系;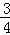 },求实数a的值.
},求实数a的值.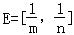 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.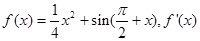 为
为 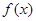 的导函数,则
的导函数,则 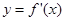 的图象大致是
的图象大致是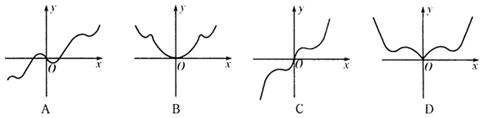
 )的单调递增区间是()
)的单调递增区间是()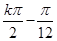 ,
,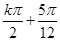 ](k∈Z)
](k∈Z)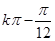 ,
,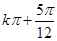 ](k∈Z)
](k∈Z)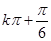 ,
,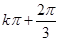 )(k∈Z)
)(k∈Z)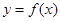 在
在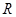 上为偶函数,当
上为偶函数,当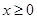 时,
时,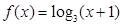 ,若
,若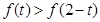 ,则实数
,则实数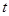 的取值范围是( )
的取值范围是( )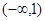
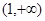
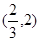
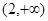
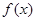 是定义在[-1,1]上的奇函数且
是定义在[-1,1]上的奇函数且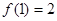 ,当
,当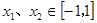 ,且
,且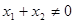 时,有
时,有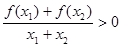 ,若
,若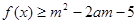 对所有
对所有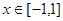 、
、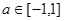 恒成立,则实数
恒成立,则实数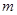 的取值范围是_________.
的取值范围是_________.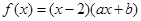 为偶函数,且在
为偶函数,且在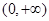 单调递增,则
单调递增,则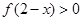 的解集为( )
的解集为( )