题目内容
【题目】过椭圆W:![]() 的左焦点F1作直线l1交椭圆于A,B两点,其中A(0,1),另一条过F1的直线l2交椭圆于C,D两点(不与A,B重合),且D点不与点0,﹣1重合.过F1作x轴的垂线分别交直线AD,BC于E,G.
的左焦点F1作直线l1交椭圆于A,B两点,其中A(0,1),另一条过F1的直线l2交椭圆于C,D两点(不与A,B重合),且D点不与点0,﹣1重合.过F1作x轴的垂线分别交直线AD,BC于E,G.
(1)求B点坐标和直线l1的方程;
(2)比较线段EF1和线段GF1的长度关系并给出证明.
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
(1)由题意得椭圆的左焦点![]() ,根据两点式可得直线
,根据两点式可得直线![]() 的方程,然后通过解方程组可得点
的方程,然后通过解方程组可得点![]() 坐标.(2)当
坐标.(2)当![]() 与
与![]() 轴垂直时易得
轴垂直时易得![]() .当
.当![]() 不与
不与![]() 轴垂直时,设
轴垂直时,设![]() 的方程为
的方程为![]() ,与椭圆方程联立消元后可得
,与椭圆方程联立消元后可得![]() ,
,![]() ,求出直线
,求出直线![]() 的方程后可得点
的方程后可得点![]() 的纵坐标
的纵坐标![]() 和点G的纵坐标
和点G的纵坐标![]() ,计算可得
,计算可得![]() ,于是
,于是![]() .
.
(1)由题意可得椭圆的左焦点![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由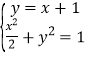 ,解得
,解得![]() 或
或 ,
,
所以点![]() .
.
(2)①当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,
,![]() 两点与
两点与![]() ,
,![]() 两点重合,由椭圆的对称性,
两点重合,由椭圆的对称性,![]() .
.
②当![]() 不与
不与![]() 轴垂直时,设
轴垂直时,设![]() 的方程为
的方程为![]() ,
,
由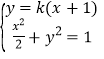 消去
消去![]() 整理得
整理得![]() ,
,
显然![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
由已知得![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得点
,得点![]() 的纵坐标
的纵坐标![]() ,
,
把![]() 代入上式得
代入上式得![]() .
.
由已知得![]() ,
,
所以直线BC的方程为 ,
,
令![]() ,得点G的纵坐标
,得点G的纵坐标![]() .
.
把![]() 代入上式得
代入上式得![]() .
.
所以![]()
![]()
![]() ,
,
又![]() ,
,
即![]() ,
,
即![]() .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目