题目内容
集合A={x|x2-3x-10<0,x∈Z},从集合A中任取两个元素a、b且a·b≠0,则方程 +
+ =1表示焦点在x轴上的椭圆的概率为________.
=1表示焦点在x轴上的椭圆的概率为________.

解析:A={x|-2<x<5,x∈Z}={-1,0,1,2,3,4},由条件知,(a,b)的所有可能取法有:(-1,1),(-1,2),(-1,3),(-1,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),(1,-1),(2,-1),(3,-1),(4,-1),(2,1),(3,1),(4,1),(3,2),(4,2),(4,3),共20种,方程 +
+ =1表示焦点在x轴上的椭圆,应有a>b>0,∴有(2,1),(3,1),(4,1),(3,2),(4,2),(4,3)共6种,∴ 所求概率P=
=1表示焦点在x轴上的椭圆,应有a>b>0,∴有(2,1),(3,1),(4,1),(3,2),(4,2),(4,3)共6种,∴ 所求概率P= =
= .
.

练习册系列答案
相关题目
某小组共有A、B、C、D、E五位同学,他们的身高(单位:m)以及体重指标(单位:kg/m2)如下表所示:
| A | B | C | D | E | |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(1) 从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
(2) 从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
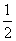 AB,BE=
AB,BE=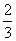 BC,若
BC,若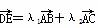 (λ1,λ2为实数),则λ1+λ2=________.
(λ1,λ2为实数),则λ1+λ2=________. (第3题图)
(第3题图)