题目内容
非零向量 、
、 满足|
满足| |=|
|=| |,且
|,且 不平行于
不平行于 ,则向量
,则向量 +
+ 与
与 -
- 的位置关系是
的位置关系是
- A.平行
- B.垂直
- C.共线且同向
- D.共线且反向
B
分析:根据两个向量的模长相等,得到两个向量的数量积为零,数量积等于零是两个向量垂直的充要条件,因此得到两个向量的关系.
解答:∵( +
+ )•(
)•( -
- )=
)=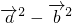 =|
=| |-|
|-| |=0,
|=0,
∴ +
+ ⊥
⊥ -
- ,
,
故选B.
点评:本题考查数量积的应用,数量积的主要应用:①求模长;②求夹角;③判垂直,本题是应用中的判垂直,解题过程中注意模长这个条件的应用,避免出错.
分析:根据两个向量的模长相等,得到两个向量的数量积为零,数量积等于零是两个向量垂直的充要条件,因此得到两个向量的关系.
解答:∵(
 +
+ )•(
)•( -
- )=
)=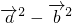 =|
=| |-|
|-| |=0,
|=0,∴
 +
+ ⊥
⊥ -
- ,
,故选B.
点评:本题考查数量积的应用,数量积的主要应用:①求模长;②求夹角;③判垂直,本题是应用中的判垂直,解题过程中注意模长这个条件的应用,避免出错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
非零向量和满足 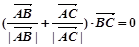 ,则△ABC为( )
,则△ABC为( )
| A.三边均不相等的三角形 | B.直角三角形 | C.等腰三角形 | D.等边三角形 |