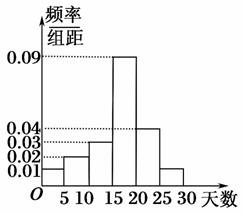
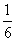题目内容
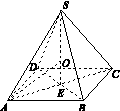
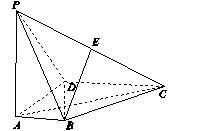
在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
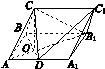
图J122
解:(1)证明:由题意可知,在Rt△ABD中,tan∠ABD=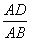 =
=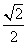 ,在Rt△ABB1中,tan∠AB1B=
,在Rt△ABB1中,tan∠AB1B=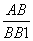 =
=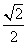 .
.
又因为0<∠ABD,∠AB1B<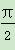 ,所以∠ABD=∠AB1B,
,所以∠ABD=∠AB1B,
所以∠ABD+∠BAB1=∠AB1B+∠BAB1=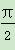 ,
,
所以AB1⊥BD.
又CO⊥侧面ABB1A1,且AB1⊂侧面ABB1A1,∴AB1⊥CO.
又BD与CO交于点O,所以AB1⊥平面CBD.
又因为BC⊂平面CBD,所以BC⊥AB1.
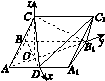
(2)如图所示,分别以OD,OB1,OC所在的直线为x轴,y轴,z轴,以O为原点,建立空间直角坐标系,
则A0,-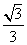 ,0,B-
,0,B-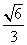 ,0,0,C0,0,
,0,0,C0,0,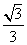 ,B10,
,B10,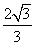 ,0,D
,0,D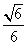 ,0,0.
,0,0.


练习册系列答案
相关题目
某射手射击所得环数X的分布列为:
| X | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 0.02 | 0.04 | 0.06 | 0.09 | 0.28 | 0.29 | 0.22 |
则此射手“射击一次命中环数大于7”的概率为( )
A.0.28 B.0.88
C.0.79 D.0.51
 B.16π C.9π D.
B.16π C.9π D.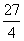
 B.
B. C.1 D.
C.1 D. B.
B.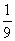
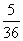 D.
D.