题目内容
如图,直角三角形 的顶点坐标
的顶点坐标 ,直角顶点
,直角顶点 ,顶点
,顶点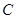 在
在 轴上,点
轴上,点 为线段
为线段 的中点
的中点

(Ⅰ)求 边所在直线方程;
边所在直线方程;
(Ⅱ)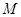 为直角三角形
为直角三角形 外接圆的圆心,求圆
外接圆的圆心,求圆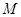 的方程;
的方程;
(Ⅲ)若动圆 过点
过点 且与圆
且与圆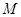 内切,求动圆
内切,求动圆 的圆心
的圆心 的轨迹方程.
的轨迹方程.
【答案】
(Ⅰ) (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ) .
.
【解析】
试题分析:(Ⅰ)∵
 1分
1分
∴ 3分
3分
∴ 5分
5分
(Ⅱ)在上式中,令 得:
得: 6分
6分
∴圆心 .
7分
.
7分
又∵ .
8分
.
8分
∴外接圆的方程为 9分
9分
(Ⅲ)∵

∵圆 过点
过点 ,∴
,∴ 是该圆的半径,
是该圆的半径,
又∵动圆 与圆
与圆 内切,
内切,
∴
即 .
.
∴点 的轨迹是以
的轨迹是以
 为焦点,长轴长为3的椭圆. 11分
为焦点,长轴长为3的椭圆. 11分
∴ ,
,
 .
12分
.
12分
∴轨迹方程为 .
.
考点:本题主要考查直线方程、圆的方程、椭圆的定义及其标准方程。
点评:中档题,本题解答思路明确,在确定轨迹方程过程中,利用了椭圆的定义。求轨迹方程的方法主要有:定义法,代入法,参数法等。本题较为容易。

练习册系列答案
相关题目
 如图,直角三角形
如图,直角三角形 的顶点坐标
的顶点坐标 ,直角顶点
,直角顶点 ,顶点
,顶点 在
在 轴上,点
轴上,点 为线段
为线段 的中点
的中点 边所在直线方程;
边所在直线方程;  (2)圆
(2)圆 是△ABC的外接圆,求圆
是△ABC的外接圆,求圆 是否是定值?
是否是定值?
