题目内容
20.已知定义在(-1,1)上的奇函数f(x),当x∈(0,1)时,f(x)=x2-1,若f(x0)=$\frac{1}{2}$,则x0=-$\frac{\sqrt{2}}{2}$.分析 利用奇函数的定义求出f(x)的解析式,令f(x0)=$\frac{1}{2}$得到方程解得.
解答 解:因为f(x)是奇函数,由x∈(0,1)时,f(x)=x2-1,当x∈(-1,0)时,f(x)=-x2+1,
所以$f({x_0})=\frac{1}{2}$时,${x_0}=-\frac{{\sqrt{2}}}{2}$.
故答案为:-$\frac{\sqrt{2}}{2}$.
点评 本题考查利用奇函数的定义求函数的解析式、解分段函数对应的方程.

练习册系列答案
相关题目
15.函数$f(x)=2sin(ωx+ϕ)(ω>0,-\frac{π}{2}<ϕ<\frac{π}{2})$的部分图象如图所示,则ω,ϕ的值为( )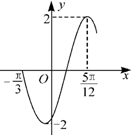

| A. | $2\;,\;\frac{2π}{3}$ | B. | $2\;,\;-\frac{π}{3}$ | C. | $1\;,\;\frac{π}{12}$ | D. | $1\;,\;-\frac{π}{12}$ |
5.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |