题目内容
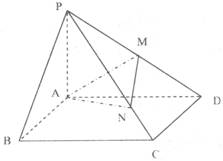 四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,且PA=AD=2AB,点M、N分别在侧棱PD、PC上,且
四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,且PA=AD=2AB,点M、N分别在侧棱PD、PC上,且![]()
(Ⅰ)求证:平面AMN⊥平面PCD;
(Ⅱ)若![]() ,求平面AMN与
,求平面AMN与
平面PAB所成二面角的余弦值。
(Ⅰ)证明:

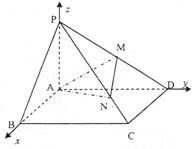 (Ⅱ)建立如图所示空间直角坐标系,设AB长为1,则
(Ⅱ)建立如图所示空间直角坐标系,设AB长为1,则
A(0,0,0),B(1,0,0),P(0,0,2),M(0,1,1),![]()
![]() 面PAB的法向量为
面PAB的法向量为
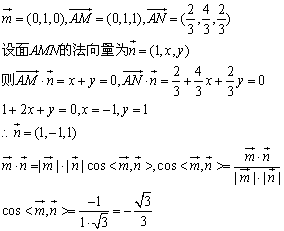
所以平面AMN与平面PAB所成二面角的余弦值为![]() 或
或![]()

练习册系列答案
相关题目
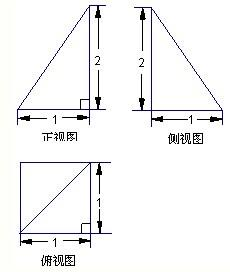 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
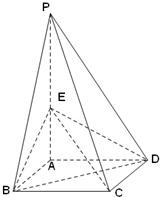 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: