题目内容
已知命题p：∀x∈[1,2]，x2－a≥0.命题q：∃x0∈R，使得x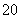
＋(a－1)x0＋1<0.若
p或q为真，p且q
为假，求实数a的取值范围．
解 ∵∀x∈[1,2]，x2－a≥0恒成立，即a≤x2恒成立，∴a≤1.即p：a≤1，∴綈p：a>1.
又∃x0∈R，使得x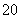＋(a－1)x0＋1<0.
∴Δ＝(a－1)2－4>0，∴a>3或a<－1，
即q：a>3或a<－1，∴綈q：－1≤a≤3.
又p或q为真，p且q为假，∴p真q假或p假q真．
当p真q假时，{a|a≤1}∩{a|－1≤a≤3}＝{a|－1≤a≤1}．
当p假q真时，{a|a>1}∩{a|a<－1或a>3}＝{a|a>3}．
综上所述，a的取值范围为{a|－1≤a≤1}∪{a|a>3}．
练习册系列答案
阅读快车系列答案
相关题目
时，s(t)<3d2成立，则d的取值范围为__________．
≥1，x∈R}，B＝{x|x2－2x－m<0}，
∩B＝{x|－1<x<4}，求实数m的值．
时，求(∁UB)∩A；
，当x≥0时，f(x)＝2x＋2x＋b(b为常数)，