题目内容
2. 如图是函数y=Asin(ωx+φ),A>0,ω>0,0<φ<$\frac{π}{2}$的图象的一部分,则它的解析式为y=2sin(2x+$\frac{π}{6}$).
如图是函数y=Asin(ωx+φ),A>0,ω>0,0<φ<$\frac{π}{2}$的图象的一部分,则它的解析式为y=2sin(2x+$\frac{π}{6}$).
分析 通过图象可以看出振幅为2,可求周期为π,利用周期公式可得ω=2,由点($\frac{11π}{12}$,0)在函数图象上,可得:2sin(2×$\frac{11π}{12}$+φ)=0,解得:φ=kπ-$\frac{11π}{6}$,k∈Z,结合范围0<φ<$\frac{π}{2}$可求φ,从而求出函数解析式.
解答 解:由图象得:A=2,T=$\frac{2π}{ω}$=$\frac{11π}{12}-(-\frac{π}{12})$=π,可得:ω=2,
∵由点($\frac{11π}{12}$,0)在函数图象上,可得:2sin(2×$\frac{11π}{12}$+φ)=0;
∴2×$\frac{11π}{12}$+φ=kπ,k∈Z,解得:φ=kπ-$\frac{11π}{6}$,k∈Z,
∵0<φ<$\frac{π}{2}$
∴解得:φ=$\frac{π}{6}$.
∴函数解析式为:y=2sin(2x+$\frac{π}{6}$).
故答案为:y=2sin(2x+$\frac{π}{6}$).
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,注意条件0<φ<$\frac{π}{2}$的应用,属于基础题.

练习册系列答案
相关题目
11.双曲线x2-4y2=8的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
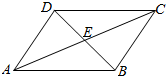 如图,在平行四边形ABCD中,$\overrightarrow{AE}$=x$\overrightarrow{AD}$+y$\overrightarrow{AB}$,则x+y=1.
如图,在平行四边形ABCD中,$\overrightarrow{AE}$=x$\overrightarrow{AD}$+y$\overrightarrow{AB}$,则x+y=1.