题目内容
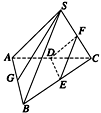
 S是正三角形ABC所在平面外的一点,如图,SA=SB=SC,且∠ASB=∠BSC=∠CSA=
S是正三角形ABC所在平面外的一点,如图,SA=SB=SC,且∠ASB=∠BSC=∠CSA=| π |
| 2 |
分析:连接MC,取MC中点为Q,连接NQ,BQ,则NQ和SM平行,∠QNB(或其补角)即为SM和BN所成的角,利用余弦定理可得结论.
解答: 解:连接MC,取MC中点为Q,连接NQ,BQ
解:连接MC,取MC中点为Q,连接NQ,BQ
则NQ和SM平行,∠QNB(或其补角)即为SM和BN所成的角.
设SA=SB=SC=a,则AB=BC=CA=
a
因为∠ASB=∠BSC=∠CSA=
,△ABC是正三角形,M、N、Q是中点
所以:NQ=
SM=
a,MC=
a,QB=
a,NB=
a
∴cos∠QNB=
=
∴异面直线SM与BN所成角的余弦值为
故选A.
 解:连接MC,取MC中点为Q,连接NQ,BQ
解:连接MC,取MC中点为Q,连接NQ,BQ则NQ和SM平行,∠QNB(或其补角)即为SM和BN所成的角.
设SA=SB=SC=a,则AB=BC=CA=
| 2 |
因为∠ASB=∠BSC=∠CSA=
| π |
| 2 |
所以:NQ=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
∴cos∠QNB=
| QN2+BN2-BQ2 |
| 2QN•BN |
| ||
| 5 |
∴异面直线SM与BN所成角的余弦值为
| ||
| 5 |
故选A.
点评:本题考查线线角,考查余弦定理,考查学生的计算能力,正确作出线线角是关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
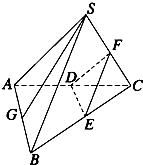 如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.
如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.