题目内容
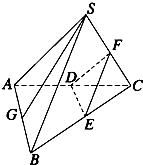如图所示，已知S是正三角形ABC所在平面外的一点，且SA=SB=SC，SG为△SAB上的高，D、E、F分别是AC、BC、SC的中点，试判断SG与平面DEF的位置关系，并给予证明．分析：如图所示，连接CG交DE于点H．在△ABC利用中位线定理证出DH∥AG，再由平行线的性质得到H为CG的中点，从而得到△SGC中FH∥SG，最后根据直线与平面平行的判定的判定定理，可证出SG∥平面DEF，得到本题答案．
解答：
解：根据题意，可得SG与平面DEF的位置关系是SG∥平面DEF，
证明如下：
如图所示，连接CG交DE于点H，
∵DE是△ABC的中位线，∴DE∥AB．
又∵在△ACG中，D是AC的中点，且DH∥AG．
∴H为CG的中点，可得FH是△SCG的中位线，
∴FH∥SG．
又∵SG?平面DEF，FH?平面DEF，
∴SG∥平面DEF．
解：根据题意，可得SG与平面DEF的位置关系是SG∥平面DEF，证明如下：
如图所示，连接CG交DE于点H，
∵DE是△ABC的中位线，∴DE∥AB．
又∵在△ACG中，D是AC的中点，且DH∥AG．
∴H为CG的中点，可得FH是△SCG的中位线，
∴FH∥SG．
又∵SG?平面DEF，FH?平面DEF，
∴SG∥平面DEF．
点评：本题在三棱锥中利用中位线定理证明了线面平行，着重考查了空间直线与平面平行的判定定理及其应用等知识，属于基础题．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
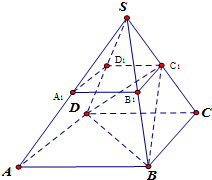如图所示，正四棱台ABCD-A1B1C1D1是由一个正三棱锥S-ABCD（底面为正方形，顶点在底面上的射影为底面正方形的中心）被平行于底面的平面截所得．已知正四棱台ABCD-A1B1C1D1下底面边长为2，上底面边长为1，高为2．
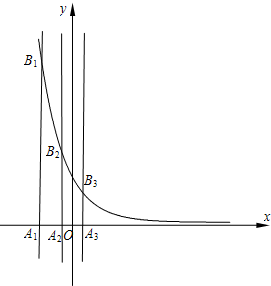（2006•蚌埠二模）已知等差数列{an}的首项为p，公差为d（d＞0）．对于不同的自然数n，直线x=an与x轴和指数函数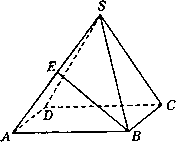
，底面边长为
，E是SA的中点，则异面直线BE与SC所成角的大小为
，底面边长为
，E是SA的中点，则异面直线BE与SC所成角的大小为 （ ）
，底面边长为
，E是SA的中点，则异面直线BE与SC所成角的大小为
（ ）