题目内容
【题目】已知函数![]() 在区间
在区间![]() 上是单调增函数,则实数
上是单调增函数,则实数![]() 的取值范围为( )
的取值范围为( )
A.  B.
B. 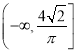 C.
C.  D.
D. 
【答案】B
【解析】令![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上恒成立,设
上恒成立,设![]() ,则
,则![]() ,再令
,再令![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 在
在![]() 上为增函数,
上为增函数,
∴![]() ∴
∴![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 在
在![]() 上减函数,∴
上减函数,∴ ,实数
,实数![]() 的取值范围为
的取值范围为 ,故选B.
,故选B.
【方法点晴】本题主要考查“分离参数”在解题中的应用、利用导数研究函数的单调性以及利用单调性求参数的范围,属于中档题. 利用单调性求参数的范围的常见方法:① 视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数需注意若函数在区间![]() 上是单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式
上是单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式![]() 或
或![]() 恒成立问题求参数范围,本题是利用方法 ② 求解的.
恒成立问题求参数范围,本题是利用方法 ② 求解的.

练习册系列答案
相关题目