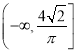题目内容
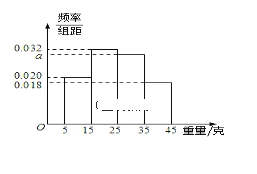
【题目】某学校随机抽取部分新生调查其上学所需时间(单位：分钟)，并将所得数据绘制成频率分布直方图(如图)，其中上学所需时间的范围是
，样本数据分组为
，
，
，
，
．
(1)求直方图中x的值；
(2)如果上学所需时间不少于1小时的学生可申请在学校住宿，若该学校有600名新生，请估计新生中有多少名学生可以申请住宿；
(3)由频率分布直方图估计该校新生上学所需时间的平均值．
【答案】(1) 
(2) 72名(3) 33.6分钟.
【解析】
（1）利用概率和为
列方程即可得解。
（2）计算出新生上学时间不少于1小时的频率为
，问题得解。
（3）直接利用均值计算公式求解即可。
解：（1）由直方图可得：
，解得.
（2）新生上学时间不少于1小时的频率为
，
因为
，所以600名新生中有72名学生可以申请住宿.
（3）由题可知
分钟.
故该校新生上学所需时间的平均值为33.6分钟.
练习册系列答案
相关题目
【题目】随机调查
名性别不同的大学生是否喜欢打羽毛球，得到如下
列联表：
男 | 女 | 总计 | |
喜欢打羽毛球 |
|
|
|
不喜欢打羽毛球 |
|
|
|
总计 |
|
|
|
临界值表：
|
|
|
|
|
|
|
|
参考公式：
（其中
）
参照临界值表，下列结论正确的是（ ）
A. 在犯错误的概率不超过
的前提下，认为“喜欢打羽毛球与性别有关”
B. 在犯错误的概率不超过的前提下，认为“喜欢打羽毛球与性别无关”
C. 在犯错误的概率不超过
的前提下，认为“喜欢打羽毛球与性别有关”
D. 在犯错误的概率不超过的前提下，认为“喜欢打羽毛球与性别无关”
