题目内容
设A是数集,且满足条件:若a∈A,a≠1,则(1)若2∈A,则A中必还有另外两个元素.
(2)集合A不可能是单元素集.
(3)集合A中至少有三个不同元素.
答案:
解析:
解析:
| 证明:所考知识点是集合中元素的性质.由a∈A,a≠1,则 (1)若2∈A,则 (2)若A为单元素集,则a= 即方程a2-a+1=0无实数解,∴ a≠ ∴ a与 (3)由已知,a∈A 现只需证明:a、 若 ∴ a≠ 若 ∴ a≠ 若 ∴ 说明:解此题的关键在于会应用集合中元素的互异性.由已知a∈A,则 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,即
,即 ,即a∈A,这样循环反复.因此说明a、
,即a∈A,这样循环反复.因此说明a、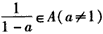 ,
,