题目内容
设A为实数集，且满足条件：若a∈A，则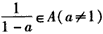
，
求证：(1)若2∈A，则A中必还有另外两个元素；
(2)集合A不可能是单元素集。
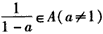，求证：(1)若2∈A，则A中必还有另外两个元素；
(2)集合A不可能是单元素集。
证明：(1)若a∈A，则
，
又∵2∈A，
∴
，
∵-1∈A，
∴
，
∵
，
∴
，
∴A中另外两个元素为-1，
。
(2)若A为单元素集，则
，
即a2-a+1=0，方程无解，
∴
，
∴A不可能为单元素集．
，又∵2∈A，
∴
， ∵-1∈A，
∴
，∵
，∴
，∴A中另外两个元素为-1，
。(2)若A为单元素集，则
，即a2-a+1=0，方程无解，
∴
，∴A不可能为单元素集．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
A，
且1??A。
∈A。
A，
且1
A。
∈A。
的定义域为实数集
，且满足
，当
时，
．则
的值为 （ ）
B．
C．0 D．1-