题目内容
由直线x=
,x=2,曲线y=
及x轴所围图形的面积为( )
| 1 |
| 2 |
| 1 |
| x |
A、
| ||
B、
| ||
C、
| ||
| D、2ln2 |
分析:由题意画出图形,再利用定积分即可求得.
解答: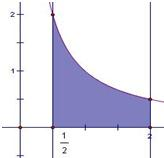 解:如图,面积S=
解:如图,面积S=
=lnx
=ln2-ln
=2ln2.
故选D.
 解:如图,面积S=
解:如图,面积S=| ∫ | 2
|
| 1 |
| x |
| | | 2
|
| 1 |
| 2 |
故选D.
点评:本题主要考查定积分求面积.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目