题目内容
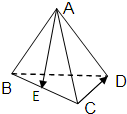
正四面体ABCD中,E、F分别是BC、AD的中点,那么EF与平面BCD所成的角的大小为
arcsin
| ||
| 3 |
arcsin
.
| ||
| 3 |
分析:欲求EF与平面BCD所成的角的大小,须先找到它的平面角,根据正四面体的性质,可知,若过F向平面BCD作垂线,垂足必在ED上,ED为EF在平面BCD上的射影,就可得到∠EFD为所求EF与平面BCD所成的角,再放入直角三角形EFD中来求角即可.
解答:解:连接DE,AE
∵ABCD为正四面体,BC⊥DE,BC⊥AE,AE=DE
∴BC⊥平面AED,平面AED⊥平面BCD
∴过F向平面BCD作垂线,则垂足必落在DE上,
∴ ∠FED为所求EF与平面BCD所成的角,
∠FED为所求EF与平面BCD所成的角,
∵AE=DE,F为AD中点,∴EF⊥AD,
∴在直角三角形EFD中,设AD=2a,则FD=a,DE=
a,
∴sin∠EFD=
=
=
∴EF与平面BCD所成的角的大小为arcsin
故答案为arcsin
∵ABCD为正四面体,BC⊥DE,BC⊥AE,AE=DE
∴BC⊥平面AED,平面AED⊥平面BCD
∴过F向平面BCD作垂线,则垂足必落在DE上,
∴
 ∠FED为所求EF与平面BCD所成的角,
∠FED为所求EF与平面BCD所成的角,∵AE=DE,F为AD中点,∴EF⊥AD,
∴在直角三角形EFD中,设AD=2a,则FD=a,DE=
| 3 |
∴sin∠EFD=
| FD |
| DE |
| a | ||
|
| ||
| 3 |
∴EF与平面BCD所成的角的大小为arcsin
| ||
| 3 |
故答案为arcsin
| ||
| 3 |
点评:本题主要考查了正四面体的性质在求线面角中的应用,综合考查了学生的空间想象力,转化能力,计算能力.

练习册系列答案
相关题目
在的棱长为1的正四面体ABCD中,E是BC的中点,则
•
=( )
| AE |
| CD |
| A、0 | ||
B、
| ||
C、-
| ||
D、-
|
在正四面体ABCD中,E、F分别为棱AD、BC的中点,连接AF、CE,则异面直线AF和CE所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在棱长为1的正四面体ABCD中,E是BC的中点,则
在棱长为1的正四面体ABCD中,E是BC的中点,则