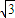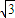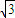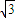题目内容
设双曲线的焦点为F1、F2,过点F2作垂直于实轴的弦PQ,若∠PF1Q=90°,则双曲线的离心率e等于( )A.
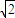 +1
+1B.
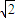
C.
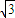
D.
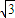 +1
+1
【答案】分析:根据题设条件我们知道PQ= ,
, 因为∠PF2Q=90°,则
因为∠PF2Q=90°,则 ,据此可以推导出双曲线的离心率.
,据此可以推导出双曲线的离心率.
解答:解:由题意可知通径|PQ|= ,
, ,
,
∵∠PF2Q=90°,∴b4=4a2c2
∵c2=a2+b2,∴c4-6a2c2+a4=0,∴e4-6e2+1=0
∴ 或
或 (舍去)
(舍去)
∴ .
.
故选A.
点评:这道题数量间的关系比较繁琐,推导过程中要多一点耐心.
 ,
, 因为∠PF2Q=90°,则
因为∠PF2Q=90°,则 ,据此可以推导出双曲线的离心率.
,据此可以推导出双曲线的离心率.解答:解:由题意可知通径|PQ|=
 ,
, ,
,∵∠PF2Q=90°,∴b4=4a2c2
∵c2=a2+b2,∴c4-6a2c2+a4=0,∴e4-6e2+1=0
∴
 或
或 (舍去)
(舍去)∴
 .
.故选A.
点评:这道题数量间的关系比较繁琐,推导过程中要多一点耐心.

练习册系列答案
相关题目
设双曲线的焦点为F1、F2,过点F2作垂直于实轴的弦PQ,若∠PF1Q=90°,则双曲线的离心率e等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则|
的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则|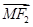 |=
|=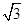 B.4
B.4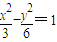 的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则|
的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则|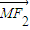 |=( )
|=( )