题目内容
设双曲线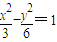
的焦点为F1、F2，过F1作x轴的垂线与该双曲线相交，其中一个交点为M，则|
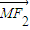|=（ ）A．5
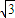
B．4
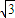
C．3
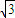
D．2
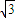
【答案】分析：依题意，可求得
-
=1的左焦点F1（-3，0），从而可求得|
|，利用双曲线的定义即可求得|
|．
解答：解：∵双曲线
-
=1中a2=3，b2=6，
∴c2=a2+b2=9，
∴c=3，故左焦点F1（-3，0）．
依题意，设M（-3，y），则
=
-1=2，
∴y=±2
，故|MF1|=2
．
∵M（-3，y）为左支上的点，
∴|MF2|-|MF1|=2
，
∴|MF2|=2
+|MF1|=4
，即|
|=4
．
故选B．
点评：本题考查双曲线的简单性质，突出定义的考查，属于中档题．
-=1的左焦点F1（-3，0），从而可求得||，利用双曲线的定义即可求得||．解答：解：∵双曲线
-=1中a2=3，b2=6，∴c2=a2+b2=9，
∴c=3，故左焦点F1（-3，0）．
依题意，设M（-3，y），则
=-1=2，∴y=±2
，故|MF1|=2．∵M（-3，y）为左支上的点，
∴|MF2|-|MF1|=2
，∴|MF2|=2
+|MF1|=4，即||=4．故选B．
点评：本题考查双曲线的简单性质，突出定义的考查，属于中档题．
练习册系列答案
相关题目
设双曲线的焦点为F1、F2，过点F2作垂直于实轴的弦PQ，若∠PF1Q=90°，则双曲线的离心率e等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
的焦点为F1、F2，过F1作x轴的垂线与该双曲线相交，其中一个交点为M，则|
|＝
的焦点为F1、F2，过F1作x轴的垂线与该双曲线相交，其中一个交点为M，则｜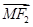
｜＝
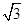B．4
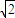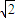
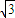
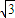+1
+1