题目内容
经过点(-2,2),且与两坐标轴所围成的三角形面积为1的直线l的方程为________.
2x+y+2=0或x+2y-2=0
分析:引入两个截距,用截距式写出方程,代入点(-2,2)得到一个关于两个截距的方程,再用截距表示出与坐标轴所围成的三角形的面积,令其为1,得到另一个关于截距的方程,解这两个方程组成方程组,求出截距,写出方程即可.
解答:设所求直线方程为 +
+ =1,由已知可得
=1,由已知可得 解得
解得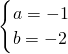 或
或 ∴2x+y+2=0或x+2y-2=0为所求.
∴2x+y+2=0或x+2y-2=0为所求.
故应填:2x+y+2=0或x+2y-2=0.
点评:考查用待定系数法求直线方程,本题先引入参数,表示出直线的方程,再根据题设的条件建立起参数的方程求参数,这是求直线方程时常用的一个思路.
分析:引入两个截距,用截距式写出方程,代入点(-2,2)得到一个关于两个截距的方程,再用截距表示出与坐标轴所围成的三角形的面积,令其为1,得到另一个关于截距的方程,解这两个方程组成方程组,求出截距,写出方程即可.
解答:设所求直线方程为
 +
+ =1,由已知可得
=1,由已知可得 解得
解得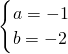 或
或 ∴2x+y+2=0或x+2y-2=0为所求.
∴2x+y+2=0或x+2y-2=0为所求.故应填:2x+y+2=0或x+2y-2=0.
点评:考查用待定系数法求直线方程,本题先引入参数,表示出直线的方程,再根据题设的条件建立起参数的方程求参数,这是求直线方程时常用的一个思路.

练习册系列答案
相关题目