题目内容
f （x）是定义在R上的奇函数，对任意x∈R总有f（x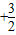
）=-f（x），则f（-
）的值为（ ）A．0
B．3
C．
D．-
【答案】分析：由f（x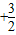
）=-f（x），可得函数的周期性，然后利用周期性和奇偶性进行求值即可．
解答：解：由f（x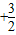
）=-f（x），得f（x+3）=f（x），所以函数的周期是3．
则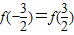
，因为函数为奇函数，所以
，
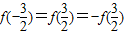所以f（-
）=0．
故选A．
点评：本题主要考查函数的周期性和奇偶性的应用，要求熟练掌握相应的函数性质，本题也可以通过赋值法进行求解．
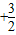）=-f（x），可得函数的周期性，然后利用周期性和奇偶性进行求值即可．解答：解：由f（x
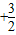）=-f（x），得f（x+3）=f（x），所以函数的周期是3．则
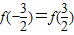，因为函数为奇函数，所以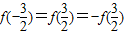，所以f（-
）=0．故选A．
点评：本题主要考查函数的周期性和奇偶性的应用，要求熟练掌握相应的函数性质，本题也可以通过赋值法进行求解．
练习册系列答案
相关题目
已知f（x）是定义在R上的不恒为零的函数，且对任意的x，y∈R都满足f（x?y）=x?f（y）+y?f（x），则f（x）是（ ）
| A、奇函数 | B、偶函数 | C、不是奇函数也不是偶函数 | D、既是奇函数又是偶函数 |