题目内容
已知向量 ,函数f(x)=a•b.
,函数f(x)=a•b.
(1)求f(x)单调递增区间;
(2)将函数f(x)图象按向量c=(m,0),得到函数y=g(x)的图象,且g(x)为偶函数,求正实数m的最小值.
解:(1)∵ =(sinx,
=(sinx, ),
), =(cosx,sin2x-
=(cosx,sin2x- ),
),
∴f(x)= •
• =sinxcosx+
=sinxcosx+ (sin2x-
(sin2x- )
)
= sin2x+
sin2x+ ×
× -
-
= sin2x-
sin2x- cos2x
cos2x
=sin(2x- ).
).
由2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ (k∈Z)得:kπ-
(k∈Z)得:kπ- ≤x≤kπ+
≤x≤kπ+ ,(k∈Z)
,(k∈Z)
f(x)的单调递增区间为:[kπ- ,kπ+
,kπ+ ],k∈Z.
],k∈Z.
(2)f(x)图象按向量 =(m,0),得到函数y=g(x)的图象,
=(m,0),得到函数y=g(x)的图象,
则:g(x)=f(x-m)=sin[2(x-m)- ]=sin(2x-2m-
]=sin(2x-2m- ),
),
∵g(x)为偶函数,
∴-2m- =kπ+
=kπ+ ,(k∈Z)
,(k∈Z)
∴当k=-1时,m最小.mmin= .
.
分析:(1)由题意可将f(x)= •
• 化为:f(x)=sin(2x-
化为:f(x)=sin(2x- ),从而利用正弦函数的单调性质即可求得f(x)单调递增区间;
),从而利用正弦函数的单调性质即可求得f(x)单调递增区间;
(2)由题意可求得g(x)=f(x-m)=sin(2x-2m- ),再结合g(x)为偶函数,可得到,-2m-
),再结合g(x)为偶函数,可得到,-2m- =kπ+
=kπ+ ,(k∈Z),于是可得正实数m的最小值.
,(k∈Z),于是可得正实数m的最小值.
点评:本题考查三角函数中的恒等变换应用,着重考查向量的数量积的坐标运算,向量的平移及函数的奇偶性的应用,综合性强,属于中档题.
 =(sinx,
=(sinx, ),
), =(cosx,sin2x-
=(cosx,sin2x- ),
),∴f(x)=
 •
• =sinxcosx+
=sinxcosx+ (sin2x-
(sin2x- )
)=
 sin2x+
sin2x+ ×
× -
-
=
 sin2x-
sin2x- cos2x
cos2x=sin(2x-
 ).
).由2kπ-
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ (k∈Z)得:kπ-
(k∈Z)得:kπ- ≤x≤kπ+
≤x≤kπ+ ,(k∈Z)
,(k∈Z)f(x)的单调递增区间为:[kπ-
 ,kπ+
,kπ+ ],k∈Z.
],k∈Z.(2)f(x)图象按向量
 =(m,0),得到函数y=g(x)的图象,
=(m,0),得到函数y=g(x)的图象,则:g(x)=f(x-m)=sin[2(x-m)-
 ]=sin(2x-2m-
]=sin(2x-2m- ),
),∵g(x)为偶函数,
∴-2m-
 =kπ+
=kπ+ ,(k∈Z)
,(k∈Z)∴当k=-1时,m最小.mmin=
 .
.分析:(1)由题意可将f(x)=
 •
• 化为:f(x)=sin(2x-
化为:f(x)=sin(2x- ),从而利用正弦函数的单调性质即可求得f(x)单调递增区间;
),从而利用正弦函数的单调性质即可求得f(x)单调递增区间;(2)由题意可求得g(x)=f(x-m)=sin(2x-2m-
 ),再结合g(x)为偶函数,可得到,-2m-
),再结合g(x)为偶函数,可得到,-2m- =kπ+
=kπ+ ,(k∈Z),于是可得正实数m的最小值.
,(k∈Z),于是可得正实数m的最小值.点评:本题考查三角函数中的恒等变换应用,着重考查向量的数量积的坐标运算,向量的平移及函数的奇偶性的应用,综合性强,属于中档题.

练习册系列答案
相关题目
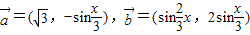 ,函数f(x)=
,函数f(x)=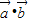 .
.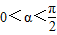 且
且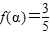 ,求
,求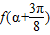 的值.
的值.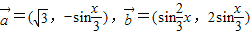 ,函数f(x)=
,函数f(x)=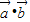 .
.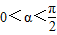 且
且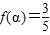 ,求
,求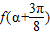 的值.
的值.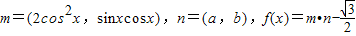 ,函数f(x)的图象关于直线
,函数f(x)的图象关于直线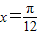 对称,且
对称,且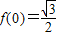
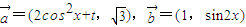 ,函数f(x)=
,函数f(x)=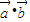 .
.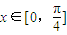 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.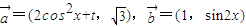 ,函数f(x)=
,函数f(x)=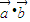 .
.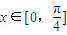 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.